-
个人简介
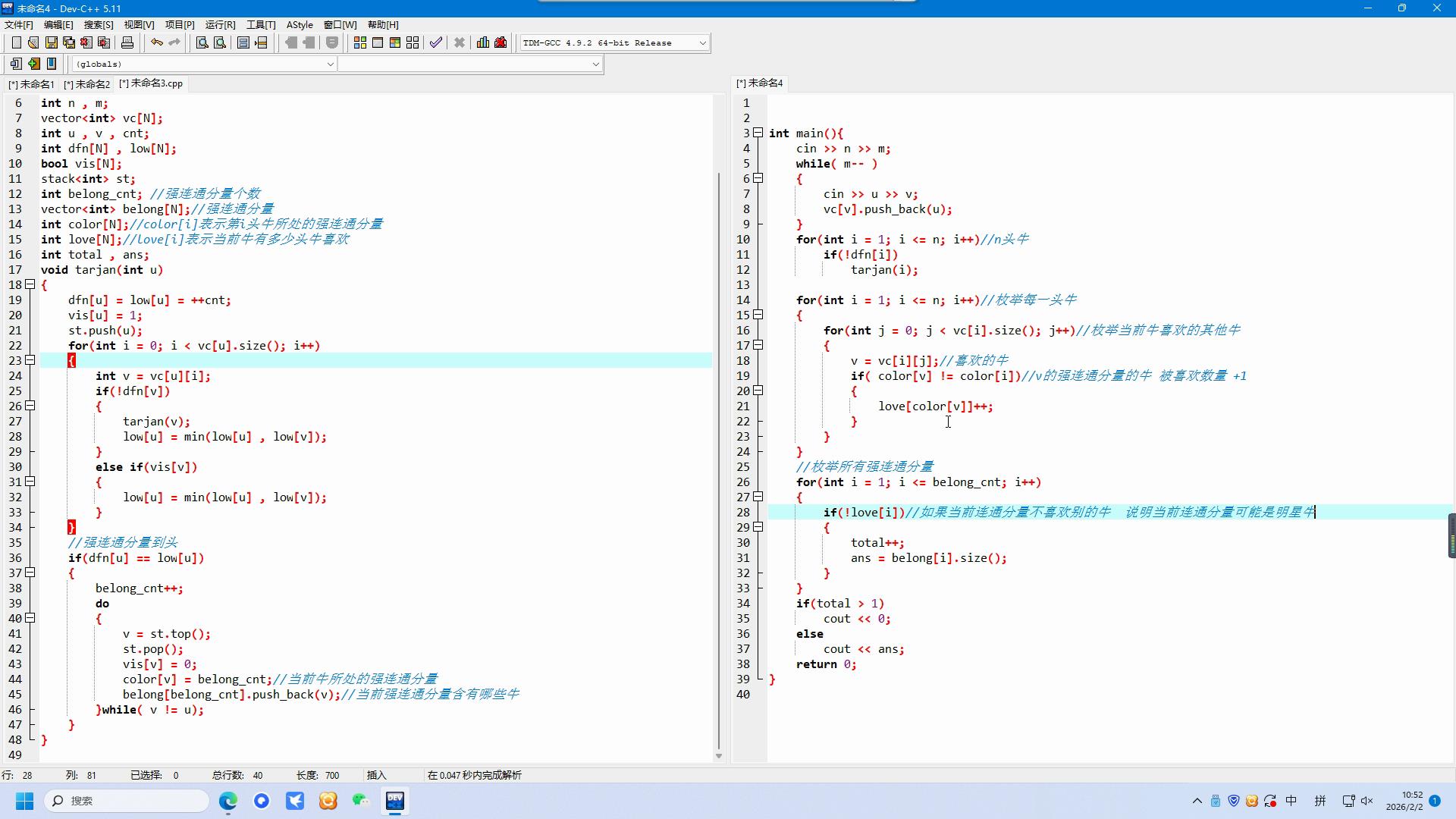
道路与航线
思路
 topsort+dijkstra
topsort+dijkstra#include<bits/stdc++.h> using namespace std; typedef pair<int, int> PII; // 定义pair类型别名,方便使用 const int N = 25010; // 最大城镇数量 const int INF = 0x3f3f3f3f; // 定义无穷大值(约10^9) int T, R, P, S; // 城镇数量,道路数量,航线数量,起点 // 使用vector实现邻接表存储图结构 // graph[u] 是一个vector,存储从节点u出发的所有边 // 每条边是一个pair:(目标节点v, 边的权重w) vector<vector<PII> > graph; // dist数组:存储从起点S到每个节点的最短距离 int dist[N]; // st数组:在Dijkstra算法中标记节点是否已确定最短路径 bool st[N]; // -------------------- 连通块相关数据结构 ------------------------------------------------------------------------------------------------------------------------------ // block[i]:存储第i个连通块中的所有节点编号 vector<int> block[N]; // id[u]:记录节点u属于哪个连通块 int id[N]; // bcnt:连通块的数量计数器 int bcnt; // visited数组:在DFS中标记节点是否已访问 bool visited[N]; // -------------------- 拓扑排序相关数据结构 ---------------------------------------------------------------------------------------------------------------------------- // din[i]:存储第i个连通块的入度(有多少条航线指向这个连通块) int din[N]; // 函数:添加一条从a到b的有向边,权重为c void add(int a, int b, int c) { // 将边(a,b)加入邻接表,权重为c graph[a].push_back(make_pair(b, c)); } // 函数:使用DFS划分连通块(只遍历道路) // 参数:u-当前节点,bid-当前连通块的编号 void dfs(int u, int bid) { // 标记当前节点已访问 visited[u] = true; // 记录当前节点属于连通块bid id[u] = bid; // 将当前节点添加到连通块bid的节点列表中 block[bid].push_back(u); // 遍历节点u的所有邻接边(道路和航线都在graph中,但DFS会遍历所有边) // 由于道路是双向的,DFS会自然地遍历整个连通分量 for (int i = 0; i < graph[u].size(); i++) { int v = graph[u][i].first; // 获取邻接节点 // 如果邻接节点还未被访问,继续DFS遍历 if (!visited[v]) { dfs(v, bid); } } } // 函数:划分所有连通块 void build_blocks() { bcnt = 0; // 初始化连通块计数器 memset(visited, false, sizeof visited); // 重置访问标记 // 遍历所有城镇 for (int i = 1; i <= T; i++) { // 如果节点i还未被访问,说明它属于一个新的连通块 if (!visited[i]) { bcnt++; // 连通块数量加1 dfs(i, bcnt); // 从节点i开始DFS,标记该连通块的所有节点 } } } // 函数:在指定连通块内运行Dijkstra算法 // 参数:bid-要处理的连通块编号 void dijkstra(int bid) { // 创建最小堆(优先队列),存储(距离, 节点)对 // greater<PII> 使队列按距离从小到大排序 priority_queue<PII, vector<PII>, greater<PII> > heap; // 将当前连通块中所有已有距离值的节点加入堆 for (int i = 0; i < block[bid].size(); i++) { int u = block[bid][i]; // 如果从起点到u的距离不是无穷大(说明已经被更新过) if (dist[u] < INF) { heap.push(make_pair(dist[u], u)); } } // Dijkstra主循环 while (!heap.empty()) { // 取出当前距离最小的节点 PII t = heap.top(); heap.pop(); int ver = t.second; // 当前节点编号 // 如果这个节点已经处理过,跳过 if (st[ver]) continue; st[ver] = true; // 标记为已处理 // 遍历当前节点的所有邻接边 for (int i = 0; i < graph[ver].size(); i++) { int v = graph[ver][i].first; // 邻接节点 int weight = graph[ver][i].second; // 边的权重 // 松弛操作:如果通过当前节点到v的路径更短,更新距离 if (dist[v] > dist[ver] + weight) { dist[v] = dist[ver] + weight; // 如果v和当前节点在同一个连通块内,将v加入堆 if (id[v] == bid) { heap.push(make_pair(dist[v], v)); } } } } } // 函数:拓扑排序处理所有连通块 void topsort() { // 初始化所有节点到起点的距离为无穷大 memset(dist, 0x3f, sizeof dist); dist[S] = 0; // 起点到自己的距离为0 // 初始化所有连通块的入度为0 memset(din, 0, sizeof din); // ---------- 第一步:计算每个连通块的入度 -------------------------------------------------------------------------------------------------------------------------- // 遍历所有城镇 for (int u = 1; u <= T; u++) { // 遍历节点u的所有出边 for (int i = 0; i < graph[u].size(); i++) { int v = graph[u][i].first; // 如果边连接的是不同连通块(即这是一条航线) if (id[u] != id[v]) { // 目标连通块的入度加1 din[id[v]]++; } } } // ---------- 第二步:初始化拓扑排序队列 ---------------------------------------------------------------------------------------------------------------------------- queue<int> q; // 用于拓扑排序的队列 // 将所有入度为0的连通块加入队列 for (int i = 1; i <= bcnt; i++) { if (din[i] == 0) { q.push(i); } } // 重置Dijkstra的标记数组 memset(st, false, sizeof st); // ---------- 第三步:按拓扑顺序处理每个连通块 ---------------------------------------------------------------------------------------------------------------------- while (!q.empty()) { int t = q.front(); // 取出一个入度为0的连通块 q.pop(); // 在该连通块内运行Dijkstra算法 dijkstra(t); // ---------- 第四步:更新相邻连通块 ---------------------------------------------------------------------------------------------------------------------------- // 遍历当前连通块的所有节点 for (int i = 0; i < block[t].size(); i++) { int u = block[t][i]; // 当前节点 // 遍历当前节点的所有邻接边 for (int j = 0; j < graph[u].size(); j++) { int v = graph[u][j].first; // 邻接节点 int weight = graph[u][j].second; // 边的权重 // 如果边连接的是其他连通块 if (id[v] != t) { // 尝试通过当前节点u更新邻接节点v的距离 if (dist[v] > dist[u] + weight) { dist[v] = dist[u] + weight; } // 拓扑排序:减少目标连通块的入度 // 因为当前连通块t已经处理完,所以指向其他连通块的边可以"移除" if (--din[id[v]] == 0) { // 如果目标连通块入度变为0,加入队列准备处理 q.push(id[v]); } } } } } } // 主函数 int main() { // ---------- 第一步:读取输入数据 ---------------------------------------------------------------------------------------------------------------------------------- cin >> T >> R >> P >> S; // 初始化邻接表,大小为T+1(因为城镇编号从1开始) graph.resize(T + 1); // ---------- 第二步:添加所有道路 ---------------------------------------------------------------------------------------------------------------------------------- // 道路是双向的,权重非负 for (int i = 0; i < R; i++) { int a, b, c; cin >> a >> b >> c; // 添加双向边 add(a, b, c); add(b, a, c); } // ---------- 第三步:划分连通块 ------------------------------------------------------------------------------------------------------------------------------------ // 只考虑道路,将图划分为多个连通分量 build_blocks(); // ---------- 第四步:添加所有航线 ---------------------------------------------------------------------------------------------------------------------------------- // 航线是单向的,权重可能为负 for (int i = 0; i < P; i++) { int a, b, c; cin >> a >> b >> c; add(a, b, c); } // ---------- 第五步:运行拓扑排序+Dijkstra算法 --------------------------------------------------------------------------------------------------------------------- topsort(); // ---------- 第六步:输出结果 -------------------------------------------------------------------------------------------------------------------------------------- for (int i = 1; i <= T; i++) { // 如果距离大于INF/2,认为不可达 // 使用INF/2而不是INF,是因为负权边更新可能使距离略小于INF if (dist[i] > INF / 2) { cout << "NO PATH" << endl; } else { cout << dist[i] << endl; } } return 0; }SPFA
#include <iostream> #include <vector> #include <queue> #include <cstring> #include <climits> using namespace std; const int MAX_T = 25005; const int MAX_RP = 150005; // R+P的最大值 const int INF = 0x3f3f3f3f; // 表示无穷大 struct Edge { int to; // 目标城镇 int cost; // 花费 Edge(int t, int c) : to(t), cost(c) {} }; int T, R, P, S; vector<Edge> graph[MAX_T]; // 邻接表 int dist[MAX_T]; // 最短距离 bool inQueue[MAX_T]; // 是否在队列中 int cnt[MAX_T]; // 入队次数,用于检测负环 // SPFA算法实现 void spfa(int start) { // 初始化距离数组 for (int i = 1; i <= T; i++) { dist[i] = INF; } dist[start] = 0; // 初始化标记数组 memset(inQueue, false, sizeof(inQueue)); memset(cnt, 0, sizeof(cnt)); queue<int> q; q.push(start); inQueue[start] = true; cnt[start] = 1; while (!q.empty()) { int u = q.front(); q.pop(); inQueue[u] = false; // 遍历所有邻接边 for (int i = 0; i < graph[u].size(); i++) { int v = graph[u][i].to; int w = graph[u][i].cost; // 松弛操作 if (dist[v] > dist[u] + w) { dist[v] = dist[u] + w; // 如果v不在队列中,加入队列 if (!inQueue[v]) { q.push(v); inQueue[v] = true; cnt[v]++; // 检测负环:如果入队次数超过T次,说明存在负环 // 但根据题目描述,不会有负环(航线不会形成环) if (cnt[v] > T) { cout << "图中存在负环!" << endl; return; } } } } } } int main() { // 输入加速 ios::sync_with_stdio(false); cin.tie(nullptr); // 读取输入 cin >> T >> R >> P >> S; // 读取道路(双向边) for (int i = 0; i < R; i++) { int a, b, c; cin >> a >> b >> c; graph[a].push_back(Edge(b, c)); graph[b].push_back(Edge(a, c)); } // 读取航线(单向边,可能有负权) for (int i = 0; i < P; i++) { int a, b, c; cin >> a >> b >> c; graph[a].push_back(Edge(b, c)); } // 运行SPFA算法 spfa(S); // 输出结果 for (int i = 1; i <= T; i++) { if (dist[i] == INF) { cout << "NO PATH" << endl; } else { cout << dist[i] << endl; } } return 0; }
toposort


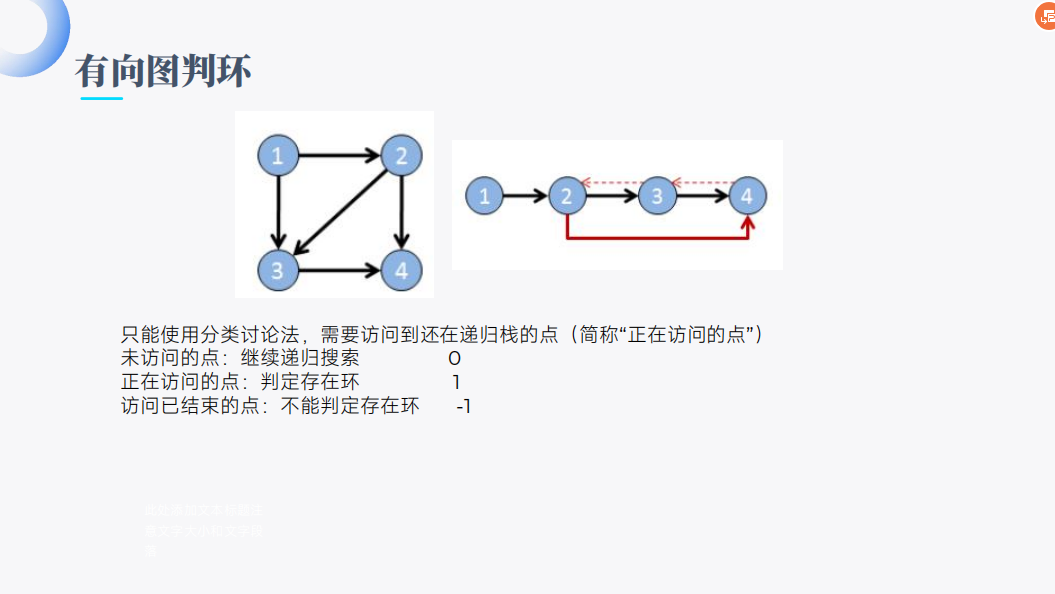
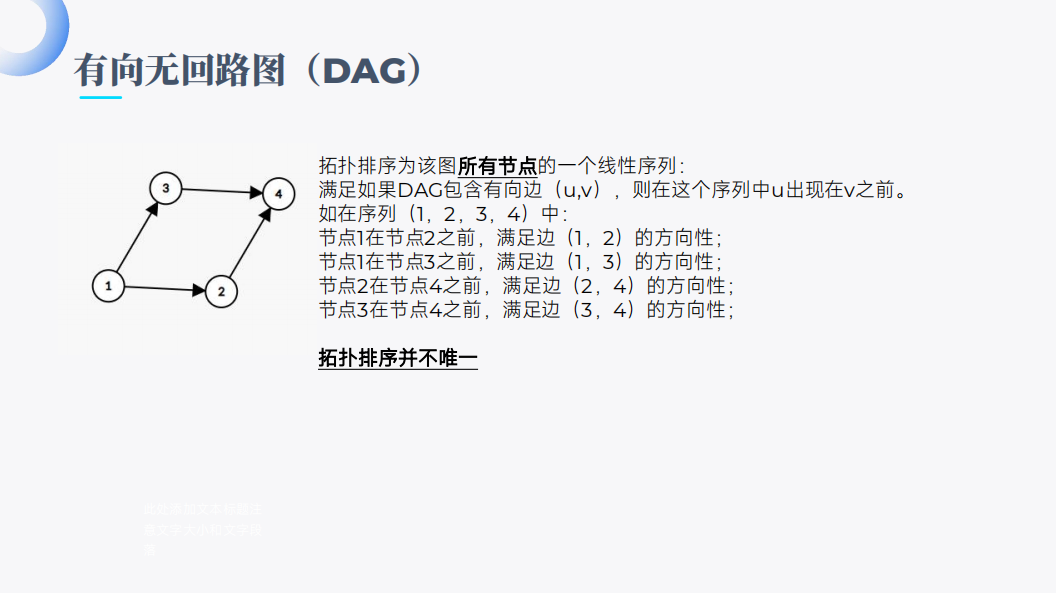



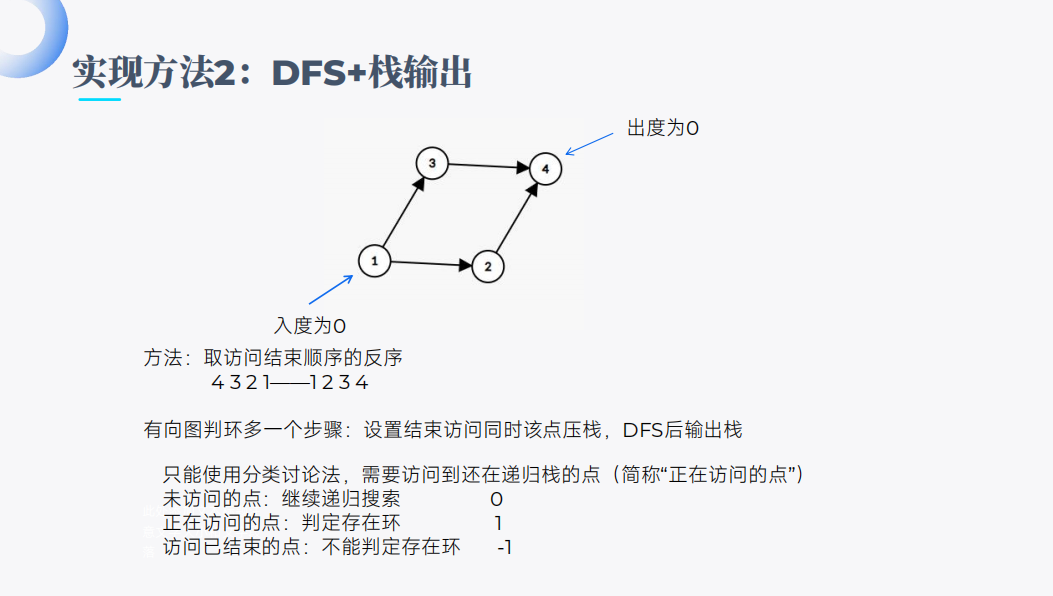

Bellman-ford与SPFA
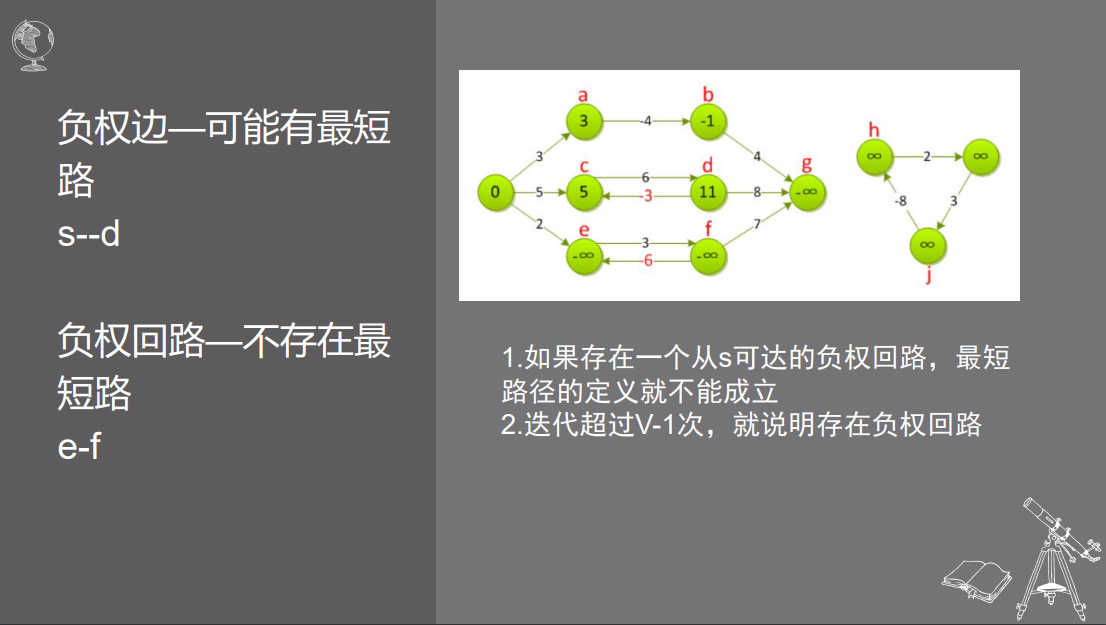
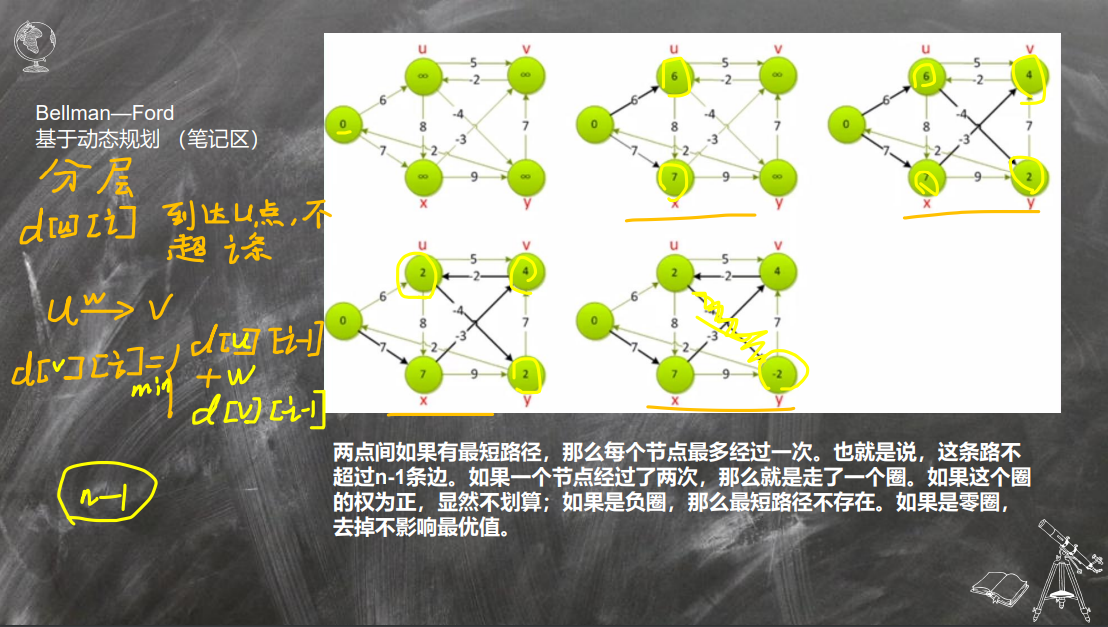

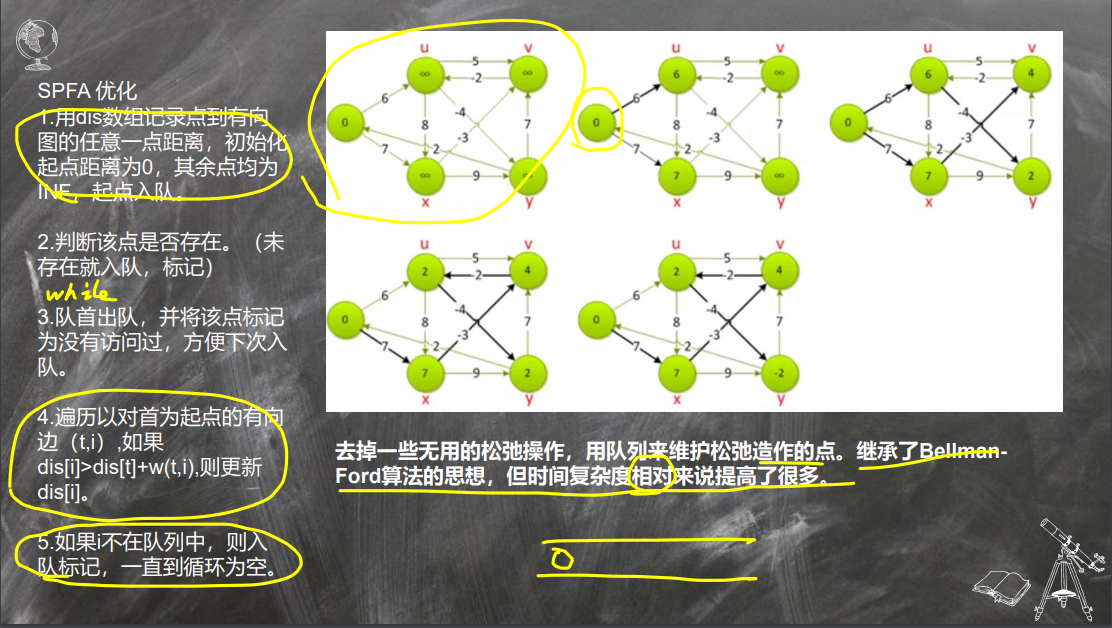
最短路
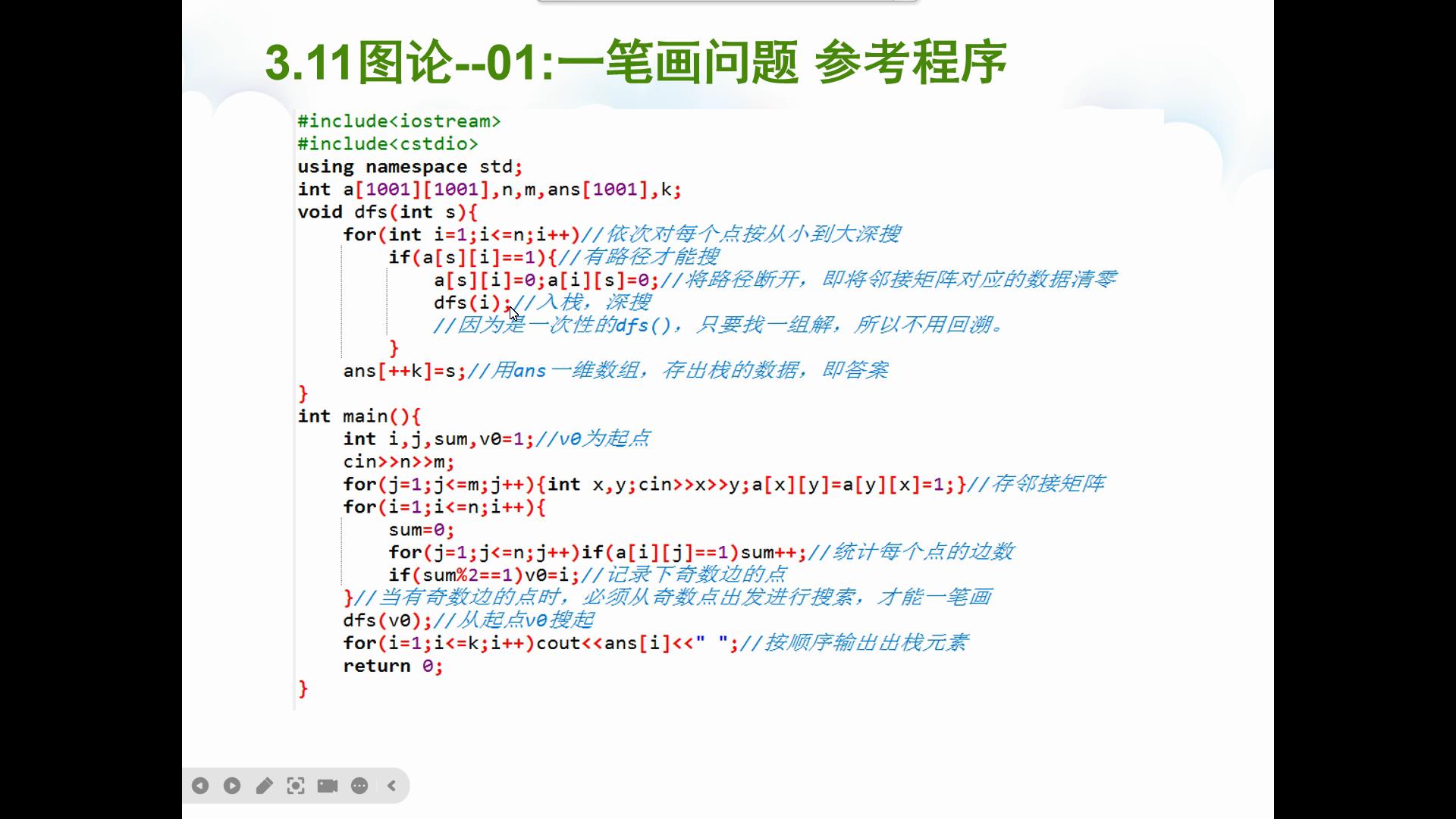
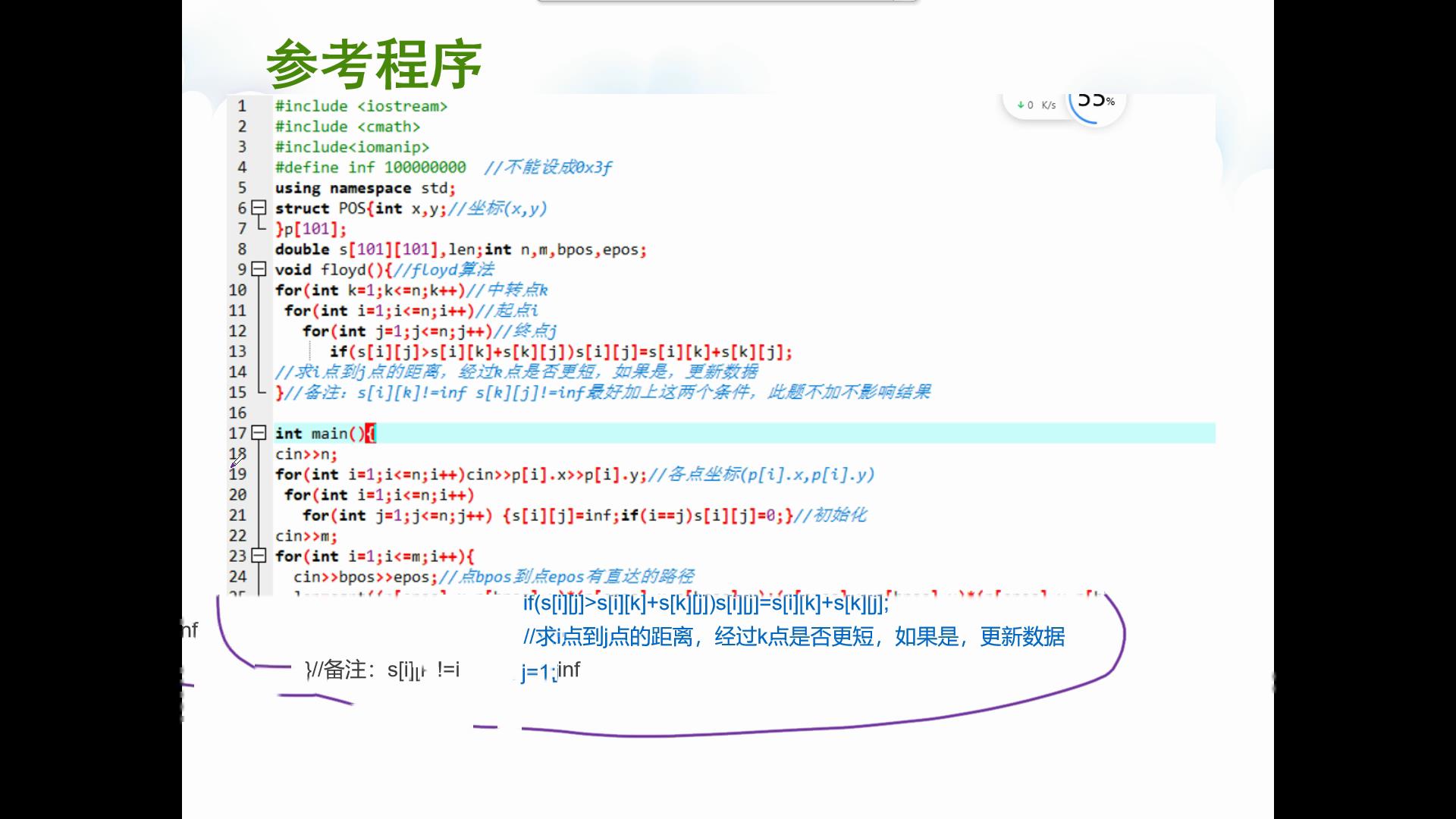
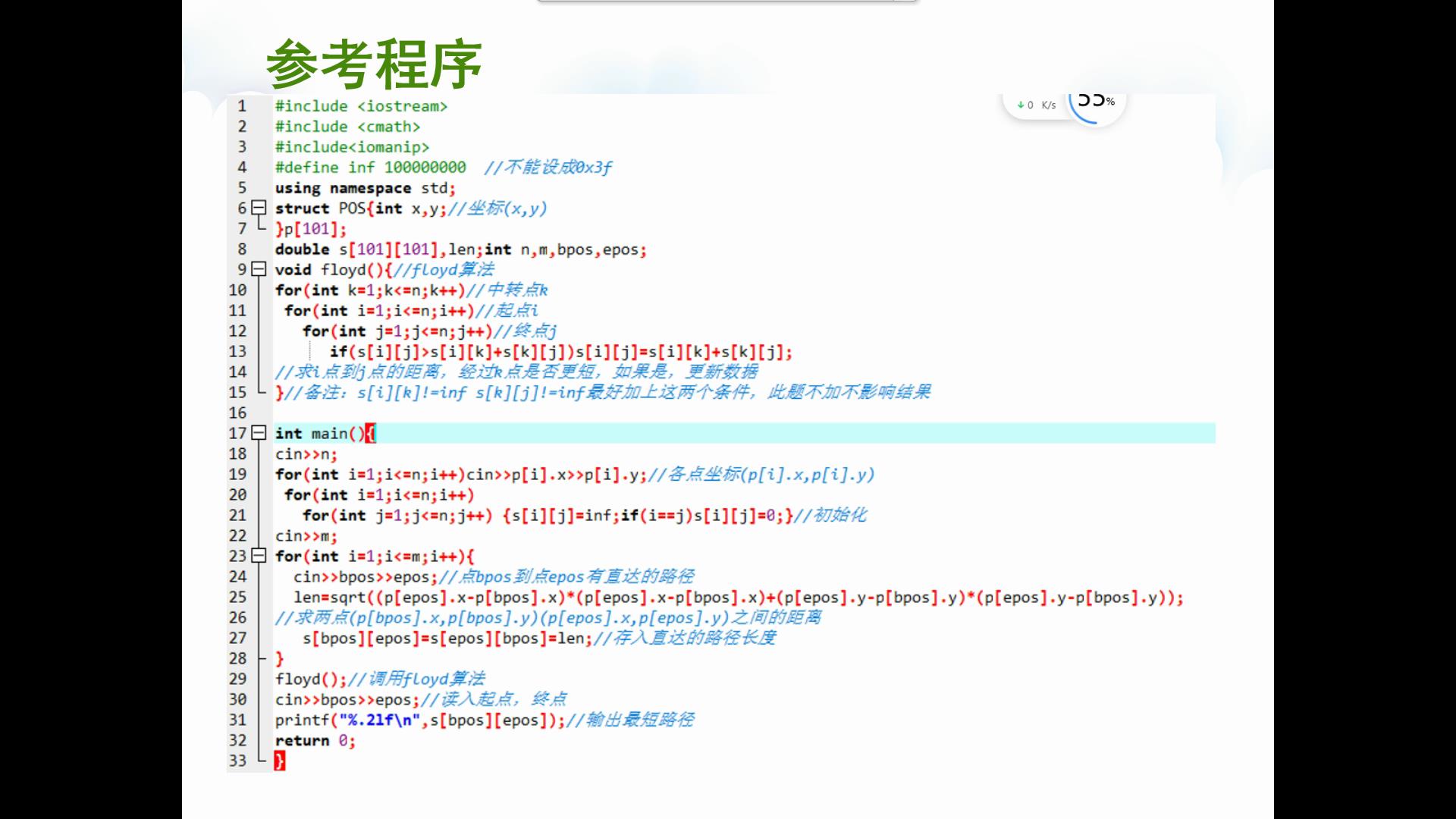
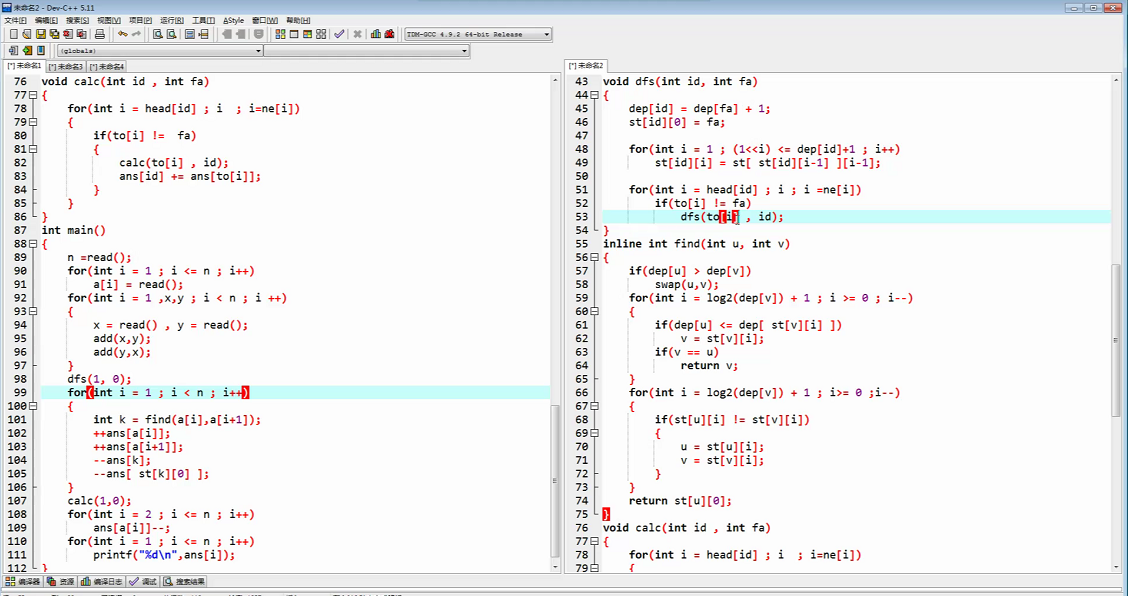

 2025 CSP-J 多边形
排序:
2025 CSP-J 多边形
排序:基数,快排,希尔 7.15
线段树(单点修改,区间查询模板):
#include<bits/stdc++.h> using namespace std; int n=0,a[114514],p=0,cnt=0,cntt=0; struct xy { int l,r,s; }; xy f[114514]; void pushup(int i) { f[i].s=f[i*2].s+f[i*2+1].s; return ; } void build(int i,int l,int r) { p++; f[i].l=l; f[i].r=r; if(l==r) { f[i].s=a[l]; return ; } int m=(l+r)/2; build(i*2,l,m); build(i*2+1,m+1,r); pushup(i); return ; } void update(int i,int l,int r) { if(f[i].l>=l&&f[i].r<=l) { f[i].s=f[i].s+r; return ; } int m=(f[i].l+f[i].r)/2; if(l<=m) { update(i*2,l,r); } if(l>m) { update(i*2+1,l,r); } pushup(i); } int main() { cin>>n; for(int i=1;i<=n;i++) { cin>>a[i]; } build(1,1,n); for(int i=1;i<=p;i++) { cout<<i<<" "<<f[i].s<<endl; } cin>>cnt>>cntt; update(1,cnt,cntt); for(int i=1;i<=p;i++) { cout<<i<<" "<<f[i].s<<endl; } }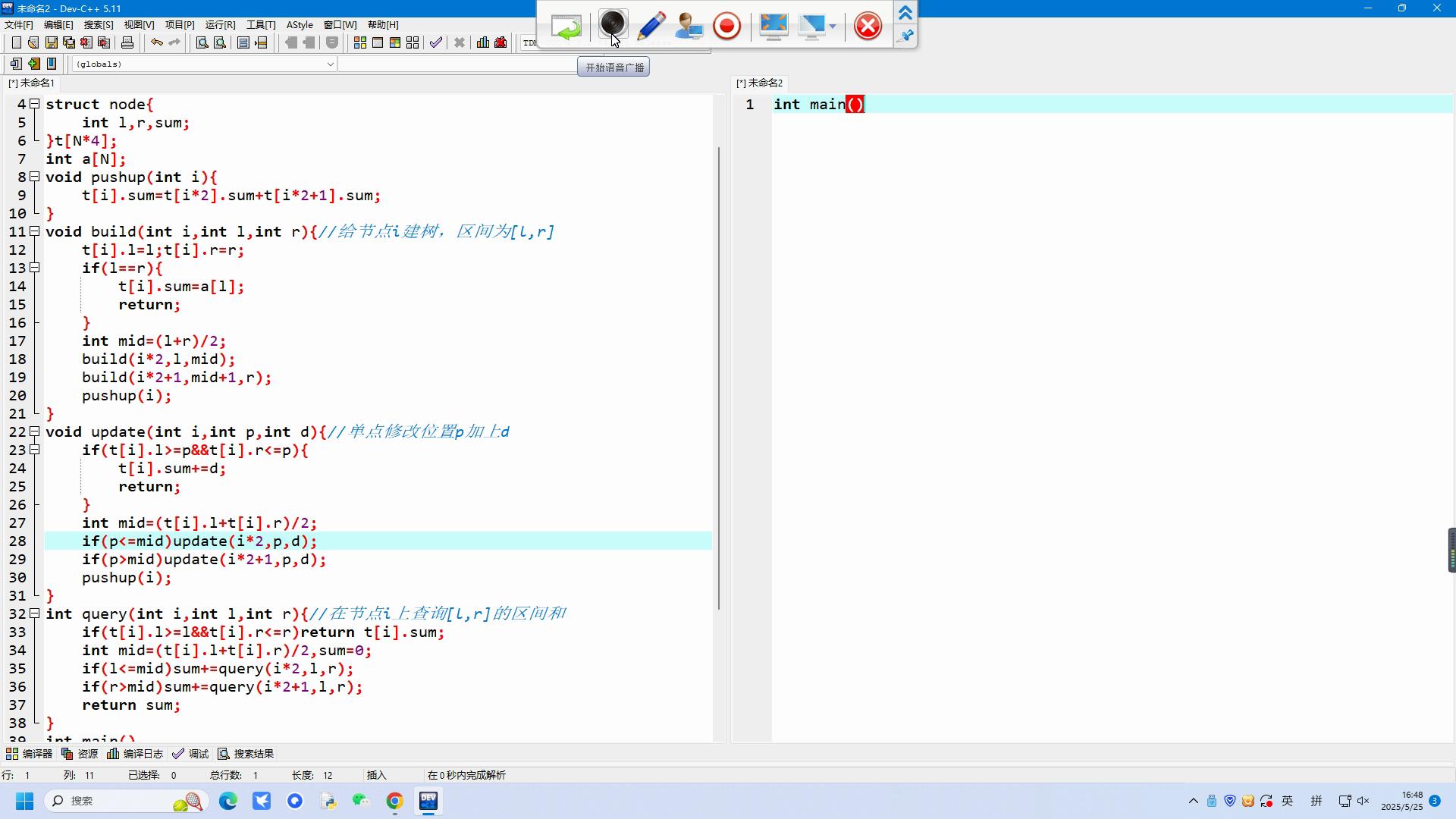
线段树(区间修改,区间查询模板):

超快速排序(代码及解析):
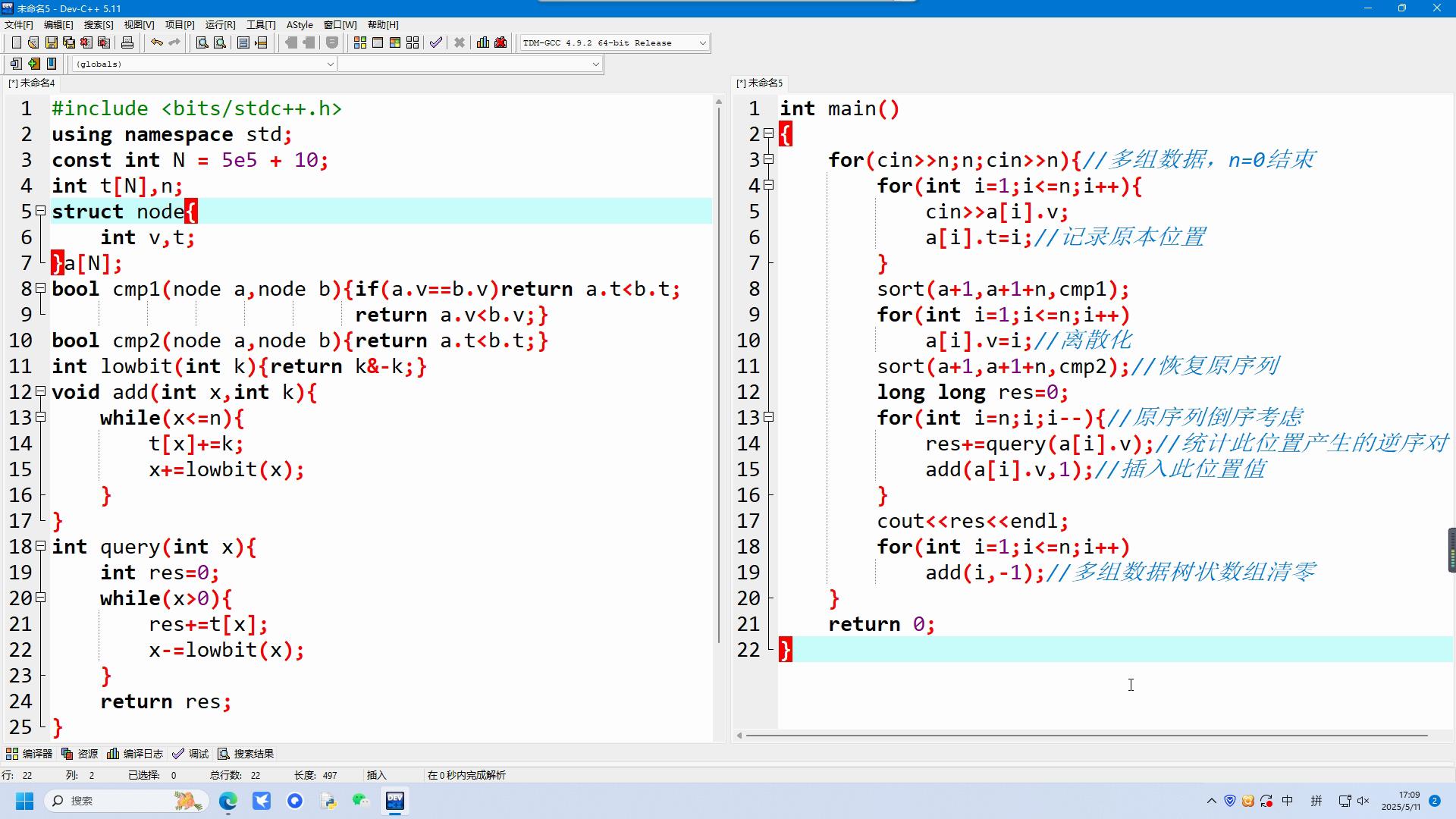
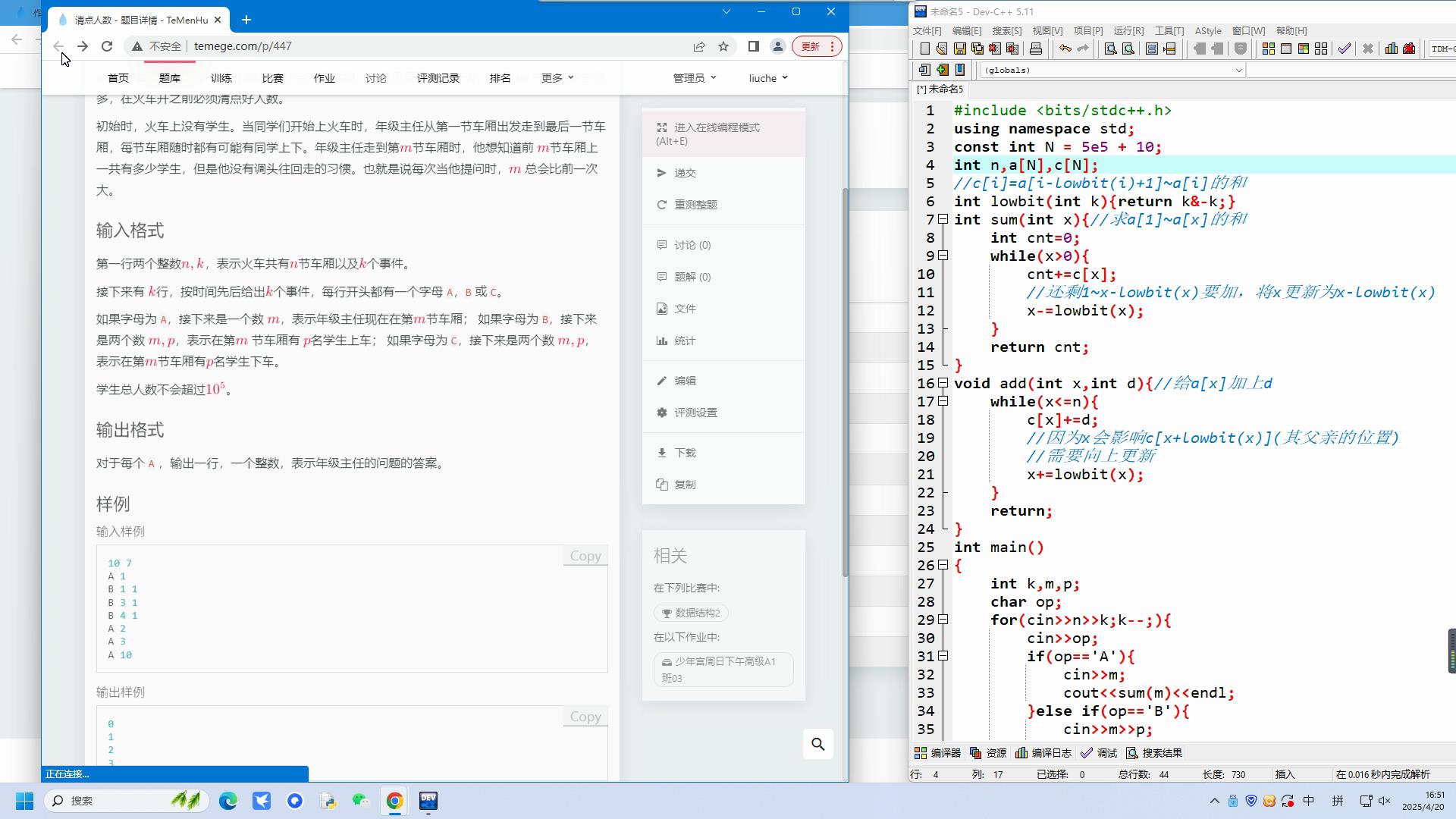

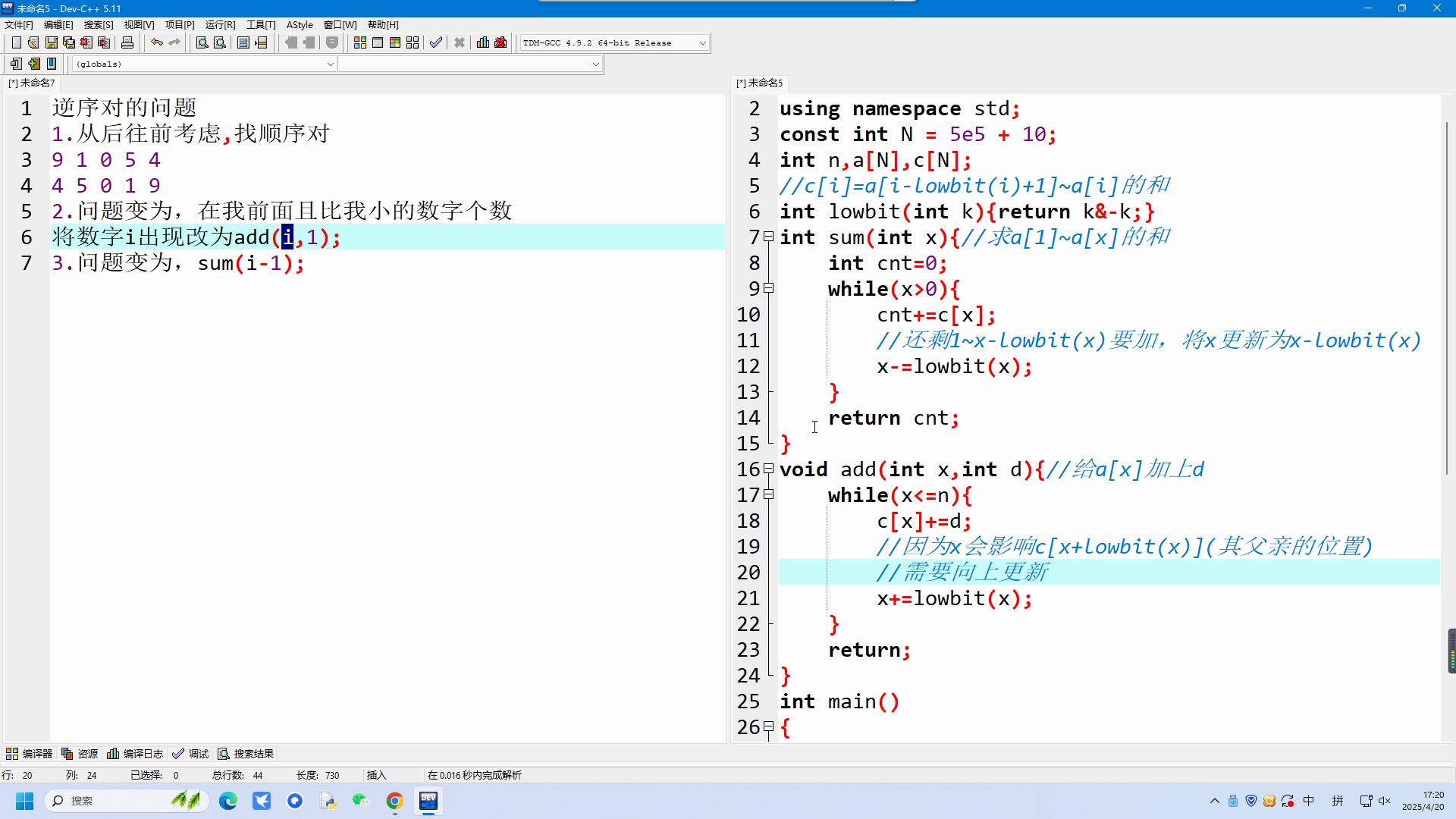
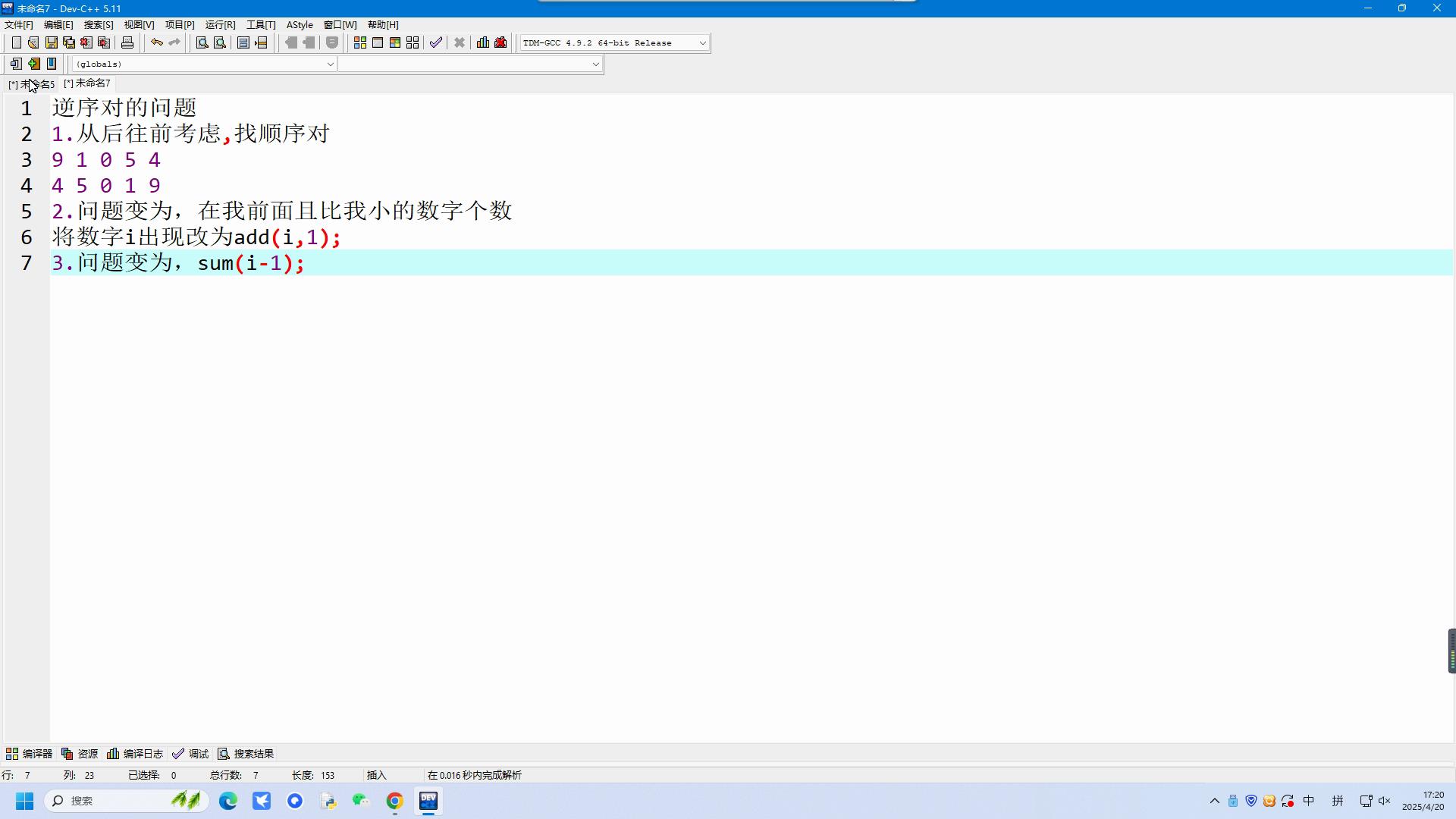


 单调栈模板
单调栈模板/*const long long N = 1e5+10,INF = 0x3f3f3f3f; long long a[N],ans[N],ans2[N],st[N],n,top,res,tmp;*/ void calc1(){ for(long long i = 1; i <= n; i++){ while(top>0&&a[i]<=a[st[top]])top--; ans[i]=st[top];st[++top]=i; }//单调栈模版,但是>=改成<=以达到效果 } void calc2(){ for(long long i = n; i >= 1; i--){ while(top>0&&a[i]<=a[st[top]])top--; ans2[i]=st[top];st[++top]=i; }//单调栈模版,但是>=改成<=以达到效果 } -
通过的题目
-
最近活动
- GESP七级编程题目 作业
- 中心团队图论练习 IOI
- 阅读量超大的CSP题目 IOI
- 少年宫周日早上初级C1班【ZZB】(for循环) 作业
- csp普专提模拟3 OI
- csp普专提模拟1(重现) OI
- csp普专提模拟 OI
- 少年宫暑期零基础day6(2025/07/10)【张正标】 作业
- 少年宫暑期零基础day5(2025/07/09)【张正标】 作业
- GESP四级真题打卡1 IOI
- 少年宫暑期零基础day3(2025/07/07)【张正标】 作业
- 少年宫暑期零基础day2(2025/07/06)【张正标】 作业
- CSP模拟题(普转提难度)2 OI
- 少年宫高级A1班小测2 IOI
- 越秀区第九届STEAM科创教育展示活动C++项目——中学组 OI
- 高级A1班小测 IOI
- 少年宫周日下午高级A1班03 作业
- 越秀区少年宫4月月测(普及组难度) OI
- 少年宫周日下午高级A1班02 作业
- 少年宫周日下午高级A1班01 作业
-
最近编写的题解
题目标签
- 动态规划
- 19
- 语言基础
- 11
- 图结构
- 10
- 数据结构
- 7
- 竞赛
- 7
- 模拟
- 5
- 其他
- 5
- NOIP
- 4
- 循环语句
- 4
- GESP四级
- 4
- GESP七级
- 4
- 单调栈
- 3
- USACO
- 3
- 最短路
- 3
- 普及组
- 3
- 排序
- 3
- 二维数组
- 3
- 背包
- 3
- Floyd
- 3
- 2005
- 2
