10 条题解

  • 2
    @ 2023-3-4 16:36:13

    这题有两个方法：

    1.表达式树

    第一步：转化为表达式树
    先转化为后缀表达式：

    定义一个列表存储 vector sf,用一个栈 stack ops存储符号

    • 数字直接加入 sf
    • 遇到 & 检查 ops的第一个是不是 &，如果是（a&b &）就将 *&*添加到 sf（ab &）,否则将 & 添加到 ops(a|b& -> abc&|)
    • 遇到 | 检查 ops的第一个是不是运算符，如果是（a&b |）就将 ops.top添加到 sf（ab &）,否则将 | 添加到 ops(a| -> ab|)
    • 如果遍历完了，将ops清空（加入sf）（a|b&c -> abc&|）
    • 括号相当于一个表达式，遇到 ( 存入ops
    • 遇到 ) 相当于遍历完了，将ops清理直到左括号（加入sf）（a&(b|c&d）-> abcd&| &)
    for(int i=0;i<s.size();i++)
	{
		if(s[i]=='1'||s[i]=='0')sf.push_back(s[i]);
		else if(s[i]=='(')ops.push('(');
		else if(s[i]==')')
		{
			while(!ops.empty()&&ops.top()!='(')
			{
				sf.push_back(ops.top());
				ops.pop();
			}
			ops.pop();
		}
		else if(s[i]=='&')
		{
			while(!ops.empty()&&ops.top()=='&')
			{
		    	sf.push_back(ops.top());
		    	ops.pop();
			}
			ops.push('&');
		}
		else
		{
			while(!ops.empty()&&ops.top()!='(')
			{
		    	sf.push_back(ops.top());
		    	ops.pop();
			}
			ops.push('|');
		}
	}
	while(!ops.empty())
	{
		sf.push_back(ops.top());
		ops.pop();
	}
    转化为表达式树：

    先定义变量

    struct node
{
	int v,l,r;//值，左节点id,右节点id 
}tr[1000005];
int num,a1,a2;//num表示tr用了几个子节点 a1 a2:dfs用
stack<int> sta;//后缀栈

    遍历 sf：

    • 无论是数字还是符号，都要放进tr[num],压入sta
    • 数字是叶子节点，l=r=-1
    • 符号的叶子从sta取出
    for(int i=0;i<sf.size();i++)
	{
		//cout << sf[i];
		if(sf[i]=='1'||sf[i]=='0')
		{
			tr[++num]={sf[i]-'0',-1,-1};//-1表示没有子节点
			sta.push(num);
		}
		else
		{
			int r=sta.top();
			sta.pop();
			int l=sta.top();
			sta.pop();
			int v=(sf[i]=='&'?2:3);
			tr[++num]={v,l,r};
			sta.push(num);
		}
	}
    第二步：dfs求解

    dfs(u)表示节点u的值：

    • tr[u]是数字直接返回
    • 不然就int l=dfs(tr[u].l)再判断有没有短路,有短路就将a1或a2++;
    • 没有短路就返回dfs(tr[u].r)

    最后调用dfs(num)得出答案

    #include <iostream>
#include <vector>
#include <stack>
using namespace std;
struct node
{
	int v,l,r;//值，左节点id,右节点id 
}tr[1000005];
int num,a1,a2;

int dfs(int u)
{
	if(tr[u].v==0||tr[u].v==1)return tr[u].v;
	int l=dfs(tr[u].l);
	if(l==0&&tr[u].v==2)//0&x
	{
		a1++;
		return 0;
	}
	if(l==1&&tr[u].v==3)//1|x
	{
		a2++;
		return 1;
	}
	return dfs(tr[u].r);
}

int main()
{
	string s;
	cin >> s;
	//树：中缀表达式转化为后缀表达式（栈） 
    vector<char> sf;
	stack<char> ops;
	stack<int> sta;
	//数字pushback->sf
	//'('pushback->ops 这样右括号配对最近的左括号 
	//')'->ops.top pushback->sf, ops.pop()
	//'&' || '|' ops!=empty&&top=='&'->push->sf
	//    else push->pos
	//最后ops.top->sf 
	for(int i=0;i<s.size();i++)
	{
		if(s[i]=='1'||s[i]=='0')sf.push_back(s[i]);
		else if(s[i]=='(')ops.push('(');
		else if(s[i]==')')
		{
			while(!ops.empty()&&ops.top()!='(')
			{
				sf.push_back(ops.top());
				ops.pop();
			}
			ops.pop();
		}
		else if(s[i]=='&')
		{
			while(!ops.empty()&&ops.top()=='&')
			{
		    	sf.push_back(ops.top());
		    	ops.pop();
			}
			ops.push('&');
		}
		else
		{
			while(!ops.empty()&&ops.top()!='(')
			{
		    	sf.push_back(ops.top());
		    	ops.pop();
			}
			ops.push('|');
		}
	}
	while(!ops.empty())
	{
		sf.push_back(ops.top());
		ops.pop();
	}

	for(int i=0;i<sf.size();i++)
	{
		//cout << sf[i];
		if(sf[i]=='1'||sf[i]=='0')
		{
			tr[++num]={sf[i]-'0',-1,-1};//-1表示没有子节点
			sta.push(num);
		}
		else
		{
			int r=sta.top();
			sta.pop();
			int l=sta.top();
			sta.pop();
			int v=(sf[i]=='&'?2:3);
			tr[++num]={v,l,r};
			sta.push(num);
		}
	}

	cout << dfs(num) << endl;
	cout << a1 << " " << a2;
	return 0;
}

    2.模拟

    模拟就简单了，只要逐步计算并且在合适的时候 打开曲速 短路跳过

    bool val;//值
int a1,a2,off;//off表示短路状态

    • 前面我们知道，只要不是短路，算式的结果就是右边的值(0 -> 0 0|1 -> 1 0|1&0 -> 0)

      if(str[i]=='1')val=1;
if(str[i]=='0')val=0;

    • 在没有短路的情况下，如果是符号就判断有没有短路

      if(val==0&&str[i]=='&')
{
	off=1;
	a1++;
}
if(val==1&&str[i]=='|')
{
	off=2;
	a2++;
}
    短路跳过

    • 若遇到左括号 ( ,就跳过括号组

      if(str[i]=='(')
{
	int x=1;
	while(x)
	{
		i++;
		if(str[i]=='(')
		{
			x++;
		}
		if(str[i]==')')x--;
	}
}

    • 或跳过(off==0)会一直到结束（前面说过，右括号等同于结束）

      else if(str[i]==')')
{
	off=0;
}

    • 与跳过(off==0)碰到 | 会结束

      else if(off==1&&str[i]=='|')
{
	off=0;
}

    • 跳过碰到同级（不在子括号里）相同符号算两个

      else if(off==1&&str[i]=='&')
{
	a1++;
}
else if(off==2&&str[i]=='|')
{
	a2++;
}

    上代码

    #include <iostream>
using namespace std;
bool val;
int a1,a2,off;

int main()
{
	string str;
	cin >> str;

	for(int i=0;i<str.size();i++)
	{
		if(off==0)
		{
			if(str[i]=='1')val=1;
			if(str[i]=='0')val=0;
			if(val==0&&str[i]=='&')
			{
				off=1;
				a1++;
			}
			if(val==1&&str[i]=='|')
			{
				off=2;
				a2++;
			}
		}
		else
		{
			if(str[i]=='(')
			{
				int x=1;
				while(x)
				{
					i++;
					if(str[i]=='(')
					{
						x++;
					}
					if(str[i]==')')x--;
				}
			}
			else if(off==1&&str[i]=='|')
			{
				off=0;
			}
			else if(str[i]==')')
			{
				off=0;
			}
			else if(off==1&&str[i]=='&')
			{
				a1++;
			}
			else if(off==2&&str[i]=='|')
			{
				a2++;
			}
		}
	}
	cout<<val<<endl<<a1<<" "<<a2;
	return 0;
}
    • 1
      @ 2023-6-9 14:48:19

      初稿(可忽略)

      这里我用一种\color{brown} 这里我用一种奇怪的输入方法\color{brown} 输入方法

      用dfs()dfs()输入。

      在dfs()dfs()里,while()while()输入,当遇到左括号(时,进入下一层dfs()dfs(),算完结果再return回去。这样就可以保证括号内先算。

      如下图(以样例为例):

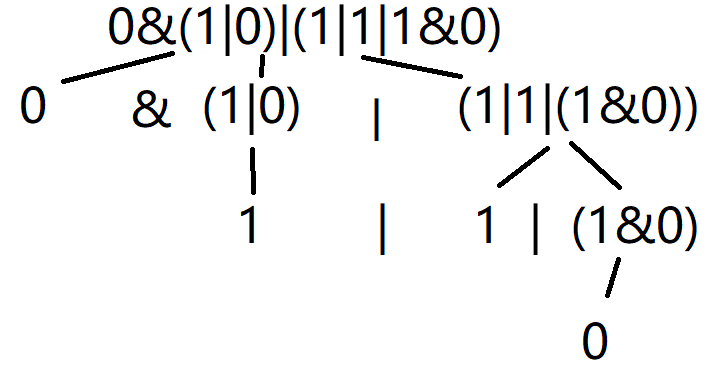
      image

      所以答案为:0⊕1∣1∣0=10⊕1|1|0=1。

      注:'⊕'符是&符。

      那么,如何算答案及回路?

      用一个字符变量fufu记录遇到的符号,输入的字符是cc,答案变量是ansans。

      • 当遇到符号时: 若c == '&',那么fu = '&'。 若c == '|',那么fu = '|'。
      • 当遇到数字时,就根据符号来更新ansans。

      关于回路,算答案时加个判断即可。

      代码:

      #include <bits/stdc++.h>
using namespace std;

int yu = 0,huo = 0;//记录与回路个数与或回路个数

int tme = 0;//debug用,记录当前下标(从1开始记)

void dfs1()//跳过括号内容函数
{
	int k = 1;//因为不能在遇到的第一个右括号处return(讲个笑话,我就s在这了)
	char c;//疯狂跳过
	while(cin >> c)
	{
		tme++;//下标更新
		if(c == '(') k++;
		if(c == ')') k--;
		if(k == 0) return;
	}
	return;
}

bool dfs()
{
	bool ans = 0;
	char fu = 'n';//记录符号(当前无符号)
	char c;
	while(cin >> c)
	{
		tme++;//下标++
		if(c == '(')//要进入下一层dfs了
		{
			if(fu == '&' && ans == 0) dfs1();//若有了回路了,那么跳过下一个括号全部内容(即不计算括号内回路)
			else if(fu == '|' && ans == 1) dfs1();//同上
			else//表示前面无回路
			{
				bool x = dfs();//计算括号内的值
				if(fu == '&') ans &= x;
				else if(fu == '|') ans |= x;//更新答案
				else ans = x;//若无符号,记得要直接赋值(讲个笑话,我又s在这儿了)
			}
		}
		else 
		{
			if(c == ')') return ans;//若遇到右括号那么直接return(因为括号包在一起算的)
		    else if(c == '&')
		    {
		    	fu = '&';//更新符号
		    	if(ans == 0) yu++;//值为0,且遇到&,回路
			}
			else if(c == '|')
			{
				fu = '|';
				if(ans == 1) huo++;//值为1,且遇到|,回路
			}
			else if(c == '0')//若为数字,更新答案
			{
				if(fu == '&') ans &= 0;
				else if(fu == '|') ans |= 0;
				else ans = 0;
			}
			else if(c == '1')//同上
			{
				if(fu == '&') ans &= 1;
				else if(fu == '|') ans |= 1;
				else ans = 1;
			}
		}
	}
	return ans;
}

signed main()
{
	cout << dfs();
	printf("\n%d %d",yu,huo);
	return 0;
}

      这题s得有点惨

      image

      对了,其实用\color{yellow} 对了,其实用表达式树做也不是不行,可以试试\color{yellow} 做也不是不行,可以试试

      • 1
        @ 2023-3-4 16:12:02

        这道题是j组第三题——逻辑表达式

        第一步，将表达式进行转换（中序表达式转后序表达式）

        需用到vector，栈and字符串中序表达式即正常方式表达后序表达式即不需要括号表达

        第二步，建表达式树

        需要结构体数组and栈

        第三步，dfs

        大家都知道，不赘述了（~~应该不用吧） ~~

        AC Code

        #include<vector>
#include<stack>
using namespace std;
string s;
const int N=1e6+5;
struct Node{
	int v,l,r;
}tr[N];
int num,ans1,ans2;
stack<char>ops;
stack<int>sta;
vector<char>sf;
void change()
{
	for(int i=0;i<s.size();i++){
		if(s[i]=='0'||s[i]=='1')sf.push_back(s[i]);
		else if(s[i]=='(')ops.push(s[i]);
		else if(s[i]==')'){
			while(!ops.empty()&&ops.top()!='('){
				sf.push_back(ops.top());
				ops.pop();
			}
			ops.pop();
		}
		else if(s[i]=='&'){
			while(!ops.empty()&&ops.top()=='&'){
				sf.push_back(ops.top());
				ops.pop() ;
			}
			ops.push('&');
		}
		else{
			while(!ops.empty()&&ops.top()!='('){
				sf.push_back(ops.top());
				ops.pop() ;
			}
			ops.push('|');
		}
	}
	while(!ops.empty()){
		sf.push_back(ops.top());
		ops.pop() ;
	}
}
void build(){
	for(int i=0;i<sf.size();i++){
		if(sf[i]=='0'||sf[i]=='1'){
			tr[++num]={sf[i]-'0',-1,-1};
			sta.push(num);
		}
		else{
			int r=sta.top();sta.pop();
			int l=sta.top();sta.pop();
			int v=(sf[i]=='&'?2:3);
			tr[++num]={v,l,r};
			sta.push(num);
		}
	}
}
int dfs(int u){
	if(tr[u].v==0||tr[u].v==1)return tr[u].v;
	int l=dfs(tr[u].l);
	if(l==0&&tr[u].v==2){
		ans1++;
		return 0;
	}
	if(l==1&&tr[u].v==3){
		ans2++;
		return 1;
	}
	int r=dfs(tr[u].r);
	return r;
}
int main(
{
	cin>>s;
	change();
	build();
	cout<<dfs(num)<<endl;
	cout<<ans1<<" "<<ans2;
	return 0;
})
        • 1
          @ 2023-3-2 20:25:31

          这道题是CSP-J的T3

          我会详细的写出解题步骤，尽量让所有人看懂 题面我就不放出来了 那么这道题思路如下↓↓↓

          第一步，把中缀表达式转换成后缀表达式

          定义

          中缀表达式就是正常人使用的表达式，包含括号、数字/变量和运算符，例如(a+b)*(b-c)-(d-c) 而后缀表达式不需要括号先是数字/变量，遇到运算符后，取出前两个值计算，将计算结果重新存入算式，代替原来的两个数字/变量和运算符，将中缀表达式的例子转换后就是ab+bc-*dc--

          需求

          首先声明一个vectorsf用来装后缀表达式，一个栈ops用来缓存符号，一个字符串s存输入的表达式 我们要让在同一个维度(括号)内,保持&在栈的位置比|高

          规则

          1. 优先级:()=1，&=2，|=3
          2. 如果是0或1，直接输出到sf中
          3. 如果是(，存入ops
          4. 如果是)，就将ops中位于最近的(之上的所有符号输出进sf，再删除(
          5. 如果是&，就从栈顶输出优先级≤&的逻辑运算符到sf(只有&)直到栈空或者遇到(或者遇到|
          6. 如果是|，就从栈顶输出优先级≤|的逻辑运算符到sf(有&和|)直到栈空或者遇到(

          注意，最后ops中还剩下一些运算符，要将其全部输出到sf 完成了转换部分，就要为后缀表达式建立表达式树

          第二步，建立表达式树

          我们需要声明一个结构体数组tr用于存放树的每个节点的值v,左子树位置l和右子树位置r，声明一个栈sta来缓存每个节点的位置

          所有叶子节点的值都为其对应的数字，用于计算 所有非叶子节点的值都为其对应运算符的值，也就是&=2，|=3 所有叶子节点的左子树和右子树位置都为-1因为叶子结点根本就没有左子树和右子树

          第三步，dfs

          我们通过dfs ~~~~(不会有人不知道深度优先搜索吧)~~~~来访问表达式树

          dfs规则

          1. 叶子结点直接返回它的值v
          2. 非叶子节点递归获取子树的值来计算
          3. 非叶子节点通过左子树判断是否出现短路，如果出现短路，直接返回左子树的值，跳过右子树

          第四步,ACCODE

          现在前三个部分的思路都清楚了，我们直接上代码:

          #include<bits/stdc++.h>
using namespace std;
string s;
struct st{
	int v,l,r;
}tr[1000001];
int num,ans1,ans2;//num是节点数量,ans1和ans2统计两种短路 
vector<char>sf;//后缀表达式 
stack<char>ops;//符号缓存 
stack<int>sta;//节点位置缓存 
void change()//中缀to后缀 
{
	for(int i=0;i<s.size();i++)
	{
		if(s[i]=='1'||s[i]=='0')//数字直接放入sf 
		{
			sf.push_back(s[i]);
		}else if(s[i]=='(')//左括号入栈 
		{
			ops.push('(');
		}else if(s[i]==')')//遇到右括号就将运算符输出到sf直到遇到左括号 
		{
			while(ops.top()!='(')
			{
				sf.push_back(ops.top());
				ops.pop();
			}
			ops.pop();//将无用的左括号出栈 
		}else if(s[i]=='&')//遇到&就将前面的&输出到sf直到栈空或者遇到其他符号 
		{
			while(!ops.empty()&&ops.top()=='&')
			{
				sf.push_back(ops.top());
				ops.pop();
			}
			ops.push('&');//将当前的&入栈 
		}else//只剩下|的情况了,将前面的&和|输出到sf直到栈空或者遇到左括号 
		{
			while(!ops.empty()&&ops.top()!='(')
			{
				sf.push_back(ops.top());
				ops.pop();
			}
			ops.push('|');//将当前的|入栈 
		}
	}
	while(!ops.empty())//将剩下的运算符入栈 
	{
		sf.push_back(ops.top());
		ops.pop();
	}
}
void build()//建立表达式树 
{
	for(int i=0;i<sf.size();i++)
	{
		if(sf[i]=='1'||sf[i]=='0')//数字存入叶子节点，值就是sf中对应的值 
		{
			tr[++num]=(st){sf[i]-'0',-1,-1};//没有子树 
			sta.push(num);//将节点位置入栈 
		}else//运算符作为非叶子节点要获取两个子节点 
		{
			int v,r,l;
			r=sta.top(),sta.pop();//从栈顶取出两个节点作为子节点 
			l=sta.top(),sta.pop();
			v=(sf[i]=='&'?2:3);//三目运算符,如果是&,值为2,否则为3 
			tr[++num]=(st){v,l,r};
			sta.push(num);//将节点位置入栈 
		}
	}
}
int dfs(int b)//开始运算 
{
	if(tr[b].v==1||tr[b].v==0)//如果是叶子节点,那么返回节点的值 
	{
		return tr[b].v;
	}
	int l=dfs(tr[b].l);//递归获取左子树返回值 
	if(l==0&&tr[b].v==2)//如果是&且满足&的短路条件,短路加一并且直接返回 
	{
		ans1++;
		return 0;
	}
	if(l==1&&tr[b].v==3)//这里是判断|的短路 
	{
		ans2++;
		return 1;
	}
	int r=dfs(tr[b].r);//获取右子树返回值 
	return r;//不满足短路,那么返回值为右子树的返回值 
}
int main()
{
	cin>>s;
	change();//中缀->后缀 
	build();//建立表达式树 
	cout<<dfs(num)<<endl;//从根节点进入dfs,dfs后的返回值就是最终结果 
	cout<<ans1<<" "<<ans2;//注意输出必须分成两次，否则短路的统计输出为0 
	return 0;
}

          以上是本蒟蒻的代码，希望您能看懂，如果有错，欢迎指出，有问题欢迎提问

          • 0
            @ 2023-3-4 16:23:26

            s1、中缀转后缀

            1，我们将其压入 vector{如果是数字，直接入后缀表达式。 }

            2，我们将其放入栈中等待匹配

            3，我们要考虑将这个右括号与先前的左括号进行匹配。那么我们就使用 while循环找左括号，在遇到左括号之前的所有运算符都直接压入 vector，因为栈是先进后出，刚好符合转后缀表达式的需要

            {如果是 ( 压入运算符栈。如果是 ) 输运算符栈不断出栈到后缀表达式，直到碰到 (。}

            4，我们同样遍历栈，如果前面遇到 & ，放入vectorvector 中.先进先出，后进后出，比较符号优先级。（优先级别：第一级是(),第二级是&,第三级是|。）

            5，不断出栈到后缀表达式。

            s2、 直接遍历这个后缀表达式,如果符号是操作数，那么我们就建立一个儿子树并将一个指向它的指针推入栈中，成一颗以操作符为根的树，其中 T1 为右儿子，T2 为左儿子；

            然后将新的树压入栈中。（根据这个运算符是 & 还是 | 对这个点进行赋值，注意和上面的 0 和 1 区分。）

            s3、遍历DFS 。

            数值 0 或 1，非叶子一定是 & 或者 | 。

            DFS ：

            遍历到叶子直接返回叶子的值；||遍历到非叶子时，先递归在返回对应的子树的值。

            然后，判断是否会短路：1| 会发生“或短路”，并且返回 1；||0& 会发生“与短路”，并且返回 0。

            非上面两种情况，计算右子树的值并返回其结果即可：0 或 1，结果都是数。

            代码：

            #include <bits/stdc++.h>

            using namespace std;

            const int N = 1e6+5;

            string s;

            struct Node{

            int v,l,r;

            } tr[N];//数组tr用于存放树的每个节点的值v,左子树位置和右子树位置l和r

            int num, ans1, ans2;

            stack ops;//运算符栈

            stack sta;//声明一个栈sta来缓存每个节点的位置

            vector sf; // sf后缀表达式

            void change(){// 中缀表达式转后缀，1、 运算符转移到sf，直到ops为空或者计算级别不同，再将此运算符push进去。

            for(int i=0;i<s.size();i++){//符号判断 

	if(s[i]=='0'||s[i]=='1')sf.push_back(s[i]); 

	else if(s[i]=='(')ops.push(s[i]); //  (，直接入运算符栈

	else if(s[i]==')') {//  )

		while(!ops.empty()&&ops.top()!='('){

			sf.push_back(ops.top()); // keepgoing，直到碰到) 

			ops.pop();

		}

		ops.pop(); // 弹出多（ 

	}

	else if(s[i] == '&') {// &

		while(!ops.empty()&&ops.top()=='&'){

			sf.push_back(ops.top());

			ops.pop();

		}

		ops.push('&');

	}

	else {//  |

		while(!ops.empty()&&ops.top() != '('){

			sf.push_back(ops.top());

			ops.pop();

		}

		ops.push('|');

	}

}

while(!ops.empty()){//整理 

	sf.push_back(ops.top());

	ops.pop();

}

            }

            void buildtree(){// 利用后缀表达式构建表达式树 2、

            for(int i=0;i<sf.size();i++){

	if(sf[i]=='0'||sf[i] == '1') {

		tr[++num]={sf[i]-'0',-1,-1};

		sta.push(num);

	}

	else{//最后将剩下的ops全部移到sf中。

		int r=sta.top();sta.pop();

		int l=sta.top();sta.pop();

		int v=(sf[i]=='&'?2:3);

		tr[++num]={v,l,r};

		sta.push(num);

	}

}

            }

            int dfs(int u){// 通过dfs (深搜)来访问表达式树并计算。

            if(tr[u].v==0||tr[u].v==1)return tr[u].v; 

int l=dfs(tr[u].l);//判断是否会短路

if(l==0&&tr[u].v == 2) {// 0&

	ans1++;

	return 0;

}

if(l==1&&tr[u].v == 3) {// 1|

	ans2++;

	return 1;

}

int r=dfs(tr[u].r); 

return r; // 不短路，结果取决于右值  1& || 0|

            }

            int main(){//简单主程序

            cin>>s;

change(); // 把中缀表达式转后缀

buildtree(); // 利用后缀表达式构建表达式树

cout<<dfs(num)<<'\n'; // 后缀表达式下，从根 dfs

cout<<ans1<<' '<<ans2;//输出 

return 0;

            }

            • 0
              @ 2023-3-4 14:35:06

              既然老师要求那就写一下题解吧，正好之前一直都不会表达式树有关的芝士。

              首先题意很明显，就不赘述了。但是这个题目看起来用直接的模拟会比较麻烦，而且越想越假。那么导致模拟麻烦的原因是什么呢？其实就时运算顺序对吧，那么接下来就要请出本次主角——后缀表达式

              首先我们拿到的这个字符串是一个中缀表达式，它有个很麻烦的点就是计算优先级。但是本期主角后缀表达式就可以很好地解决这个问题，因为后缀表达式是没有括号的，而且计算优先级很明显（当然是对于计算机来说），从而可以更方便地计算。

              那么首先要说地就是如何将中缀表达式转换成后缀表达式

              对于输入的字符串，我们有 5 种可能：

              1.这是数字，即 0或 1

              1. 这是左边的括号

              3.这是右边的括号

              4.这是 & 运算符

              1. 这是 |∣ 运算符

              然后再回想一下中缀是怎么转后缀的，首先我们需要一个栈（用于存储括号或者运算符）与一个存储表达式的结果的 vector

              对于情况 1，我们直接将其压入 vector

              对于情况 2，我们将其放入栈中等待匹配

              对于情况 3，我们要考虑将这个右括号与先前的左括号进行匹配。那么我们就使用 while循环找左括号，在遇到左括号之前的所有运算符都直接压入 vector，因为栈是先进后出，刚好符合转后缀表达式的需要

              对于情况 4，我们同样遍历栈，如果前面遇到 & ，那么就放入我们的 vectorvector 中，因为遇到的 & 就说明遇到比自己更早或者同时要进行运算的运算符，所以要先放进去

              对于情况 5，遍历栈，如果遇到左括号就停止。

              对于人来说，这并没有简便多少；但是对于计算机来说，至于要从左往右将两个数用后面的一个运算符进行运算即可。

              那么转好了后缀之后还是不行，因为还是不好算。所以我们还需要建表达式树。

              struct node{
	int v,l,r;// 值 || 左儿子 || 右儿子
}tr[N];

              我们直接遍历这个后缀表达式，如果遇到了 数字 ， 那么就直接建立一个节点，并且将其放入栈中。如果遇到的是运算符，那么就从栈里面取出两个数，建为右儿子和左儿子，然后根据这个运算符是 & 还是 | 对这个点进行赋值，注意和上面的 0 和 1 区分。

              树建好后就开始深搜遍历整棵树并且进行计算。首先如果这个点它是叶子节点 ， 即代表数字 ， 那么直接返回该节点的值。因为我们还要进行短路的计算，所以要先看左儿子和该节点的运算符是否构成短路 。那么短路之后我们可以直接返回左儿子计算的值，因为如果不短路 ， 那么本次计算的结果就取决于右儿子的值。

              怎么证明呢？有个很好的证明方法：

              首先考虑数值与符号有几种构成方式 无非就 0& // 0| // 1& // 1| 四种那么反过来也一样 所以如果前面的这个数它与运算符不构成短路，那么后面的这个数和运算符 一定是可以构成短路的 （当然按照题目意思是不能计算再在短路计数中的） 所以最后如果不能短路那么久取决于右儿子的值

              讲了那么多， ~相信你也没咋懂~ ，那么

              OK上代码（

              #include <bits/stdc++.h>
using namespace std;
const int N = 1e6+10;
int n ,  ans1 , ans2 ,x,y;
struct node{
	int v,l,r;
}tr[N];
int num;
stack<char> ops;
vector<char> sf;
string s; 
stack<int> sta;
void change(){
	for(int i=0;i<n;i++){
		if(s[i] == '0' || s[i] == '1') sf.push_back(s[i]);
		else if(s[i] == '(') ops.push(s[i]);
		else if(s[i] == ')'){
			while(!ops.empty() && ops.top() != '('){
				sf.push_back(ops.top());
				ops.pop();
			}
			ops.pop();
			
		}
		else if(s[i] == '&'){
			while(!ops.empty() && ops.top() == '&'){
				sf.push_back(ops.top());
				ops.pop();
			}
			ops.push('&');
		}
		else if(s[i] == '|'){
			while(!ops.empty() && ops.top() != '('){
				sf.push_back(ops.top());
				ops.pop();
			}
			ops.push('|');
		}
	}
	while(!ops.empty()){
		sf.push_back(ops.top());
		ops.pop();
	}
}
void build(){

	for(int i=0;i<sf.size();i++){
		if(sf[i] == '0' || sf[i] == '1') {
			tr[++num] = {sf[i] - '0' , -1 , -1};
		//	cout << sf[i] << endl;
			sta.push(num);
		}
		else{
			int r = sta.top() ; sta.pop();
			
			int l = sta.top() ; sta.pop();
			
			int v = (sf[i] == '&') ? 2 : 3;
			tr[++num] = {v , l , r};
			sta.push(num);
		}
	}
}
int dfs(int u){
	if(tr[u].v == 0 || tr[u].v == 1) return tr[u].v;
	int l = dfs(tr[u].l) ;
//	cout << ans1 << " " << ans2 << endl;
	if(l == 0 && tr[u].v == 2){
		ans1++;
	//	x = max(x , ans1);
		return 0;
	}
	if(l == 1 && tr[u].v == 3){
		ans2++;
	//	y =  ans2;
		return 1;
	}
	int r = dfs(tr[u].r); //没有短路， 结果取决于r
	return r;
	
}
int main(){
	cin >> s;
	n = s.size();
	change();
	build();
	int t = dfs(num);
	cout << t << endl << ans1 << " " << ans2; 
	return 0; 
}

              谢谢观看 QwQ !

              • 0
                @ 2023-3-4 12:16:11

                题目分析：

                我们需要让计算机计算这一条逻辑表达式的值，并计算短路的个数。

                首先，短路分为两种：

                1. 与短路：0&---------的结果一定是0；

                2. 或短路：1|---------的结果一定是1；

                  ​以0&(1|0)|(1|1|1&0)为例​, 短路情况：0& 1| 1|

                其次，我们需要将中缀表达式改写成后缀表达式：

                用一个vector记录后缀表达式sf，用一个stack记录操作符ops;

                具体扫描规则如下：

                1. 优先级别：第一级是(),第二级是&,第三级是|。
                2. 遇到数字时，将数字push进sf;
                3. 遇到(时，将( push进ops;
                4. 遇到)时，将上一个（前的运算符全部转移到sf中，ops pop掉（。
                5. 遇到运算符时，将运算符转移到sf，直到ops为空或者计算级别不同，再将此运算符push进去。

                最后将剩下的ops全部移到sf中。

                如扫描1|(1|1)&(0&1)​:

                • 扫到1，ops不变，sf为1；
                • 扫到|，ops为|，sf不变；
                • 扫到(，ops为|(，sf不变；
                • 扫到1，ops不变，sf为11；
                • 扫到|，ops为|(|，sf为不变；
                • 扫到1，ops不变，sf为111；
                • 扫到)，ops为|，sf为111|；
                • 扫到&，ops为|&，sf不变；
                • 扫到(，ops为|&(，sf不变；
                • 扫到0，ops不变，sf为111|0；
                • 扫到&，ops为|&(&，sf不变；
                • 扫到1，ops不变，sf为111|01;
                • 扫到)，ops为|&，sf为111|01&；
                • 最后，sf为111|01&&|

                然后，我们需要将中缀表达式转换成表达式树：

                ​我们需要声明一个结构体数组tr用于存放树的每个节点的值v,左子树位置和右子树位置l和r，声明一个栈sta来缓存每个节点的位置

                所有叶子节点的值都为其对应的数字，用于计算​。​所有非叶子节点的值都为其对应运算符的值，也就是按照运算优先级的顺序：&=2,|=3,所有叶子节点的左子树和右子树位置都为-1,因为叶子结点根本就没有左子树和右子树.

                ​最后，我们通过dfs (深搜)来访问表达式树并计算。

                具体访问规则如下：

                1. 若访问节点的`l`和`r`都是`-1`，直接返回`v`，否则进入第二点；
                2. 计算左节点的数值；
                3. 判断是否出现短路情况，如出现直接返回对应数值；
                4. 计算并返回右节点的数值。

                代码:

                #include<iostream>
#include<vector>
#include<stack>
using namespace std;
string s;
const int N=1e6+5;
struct Node{
       int v,l,r;
}tr[N];
int num,ans1,ans2;
stack<char>ops;
stack<int>sta;
vector<char>sf;
void change()*//* *中缀表达式转后缀表达式* 
{
       for(int i=0;i<s.size();i++)
       {
              if(s[i]=='0'||s[i]=='1') sf.push\_back(s[i]);   *​//​*​*扫到数字，直接插入*​*sf*
              else if(s[i]=='(')  ops.push(s[i]);  *//*  *扫到左边括号，插入运算符栈*
              else if(s[i]==')') 
              {
                    while(!ops.empty()&&ops.top()!='(')
                    {
                           sf.push\_back(ops.top());*//* *一直输出到*​​*sf*​​*。直到遇上*​*( *
                           ops.pop();
                    }
                    ops.pop();  *//* *输出多余的（* 
              } 
              else if(s[i]=='&')
              {  *​//​*​*与运算*
                   while(!ops.empty()&&ops.top()=='&')
                     {
                     sf.push\_back(ops.top());
                     ops.pop();
                     }
                     ops.push('&');
              }
              else
              {    *​//​*​*或运算* 
                     while(!ops.empty()&&ops.top()!='(')
                    {
                            sf.push\_back(ops.top());
                            ops.pop();

                     }
                     ops.push('|');
              }
       }
       while (!ops.empty())
       {
              sf.push\_back(ops.top());
              ops.pop();
       }
}
void build()
{
       for(int i=0;i<sf.size();i++)
       {
              if(sf[i]=='1'||sf[i]=='0')
              {
                    tr[++num]={sf[i]-'0',-1,-1};
                    sta.push(num);
              }
              else
              {
                    int r=sta.top(); sta.pop();
                    int l=sta.top(); sta.pop();
                    int v=(sf[i]=='&'?2:3);
                    tr[++num]={v,l,r};
                    sta.push(num);
              }
       }
}
int dfs(int u)
{
​       if(tr[u].v==0||tr[u].v==1) return tr[u].v; *​//​*​*叶子节点* *。返回数值* 
​       int l=dfs(tr[u].l);
       if(l==0&&tr[u].v==2)
       {*//0&*
       ans1++;
          return 0; 
       }
       if(l==1&&tr[u].v==3)
       {*//1|*
              ans2++;
              return 1; 
       }
       int r=dfs(tr[u].r);
       return r;
}
int main()
{
       cin>>s;
       change();
       build();
       cout<<dfs(num)<<endl;
       cout<<ans1<<" "<<ans2;
       return 0;
 }
                • 0
                  @ 2023-3-2 20:13:25

                  题目大意

                  - 给定一个只含0、1、&（与运算）、|（或运算）、（、 ）的表达式。

                  - 计算表达式时，应采用“短路”的思想：

                  1. &：0&n=0，称之为&的一次“短路”。（&的定义）
                  2. |：1|n=1，称之为|的一次“短路”。（|的定义）

                  （c++逻辑运算符大全及用法）

                  思路

                  Step0:定义结构体、栈、队列（栈的定义 队列的定义）

                  struct Node{//结构体定义
	int v,l,r;
}tr[N];

                  //stack：栈
//vector：队列
stack<char>ops;//运算符栈
stack<int>sta;//数字栈
vector<char>sf;//数字队列

                  Step1:中缀表达式转后缀表达式 （中缀和后缀表达式的定义）

                  我们首先遍历表达式。

                  每次遍历有5种可能：

                  1. 数字。如果是数字，直接存入sf。
                  2. 左括号。直接把左括号存入ops。
                  3. 右括号。如果扫到右括号，那就一直输出sf，直到遇到左括号，最后输出多余的左括号。
                  4. 与（&）。同扫到右括号的情况差不多，只不过最后输出的是多余的&号。
                  5. 或（|）。同扫到右括号、与（&）的情况差不多，只不过最后输出的是多余的|号。

                  最后把sf全部输出即可。

                  void change()// 中缀表达式转后缀表达式 
{
	for(int i=0;i<s.size();i++){
		if(s[i]=='0'||s[i]=='1') sf.push_back(s[i]);   //扫到数字，直接插入sf
		else if(s[i]=='(')  ops.push(s[i]);  //  扫到左边括号，插入运算符栈
		else if(s[i]==')') {
			while(!ops.empty()&&ops.top()!='('){
				sf.push_back(ops.top());// 一直输出到sf。直到遇上( 
				ops.pop();
			}
			ops.pop();  // 输出多余的（ 
		} 
		else if(s[i]=='&'){  //与运算
		     while(!ops.empty()&&ops.top()=='&'){
		     	sf.push_back(ops.top());
		     	ops.pop();
			 }
			 ops.push('&');
	    }
	    else{    //或预算 
	    	while(!ops.empty()&&ops.top()!='('){
		     	sf.push_back(ops.top());
		     	ops.pop();
			 }
			 ops.push('|');
		}
	    
	}
	while (!ops.empty()){
		sf.push_back(ops.top());
		ops.pop();
	}
}

                  Step2:建立表达式树（表达式树的定义）

                  首先，我们依次读入sf中的每个数，判断是否为操作数。（如果不知道什么是操作数，请按这里）

                  如果是，那就把它（操作数的指针）推入栈中。

                  如果不是，弹出两棵树A和B,形成一棵以操作数为根的树，将新树压入栈中。

                  void build()
{
	for(int i=0;i<sf.size();i++){
		if(sf[i]=='1'||sf[i]=='0'){
			tr[++num]={sf[i]-'0',-1,-1};
			sta.push(num);
		}
		else{
			int r=sta.top(); sta.pop();
			int l=sta.top(); sta.pop();
			int v=(sf[i]=='&'?2:3);
			tr[++num]={v,l,r};
			sta.push(num);
		}
	}
}

                  Step3:深搜（深度优先搜索DFS）找到答案

                  DFS：

                  1. 判断是否为叶子结点，如果是，返回数值。
                  2. &的“短路”。
                  3. |的“短路”。
                  如果上面三种都不符合，结果取决于r。
                  int dfs(int u)
{
	if(tr[u].v==0||tr[u].v==1) return tr[u].v; //叶子节点 。返回数值 
	int l=dfs(tr[u].l);
	if(l==0&&tr[u].v==2) {//0&
       ans1++;
	   return 0; 
	}
	if(l==1&&tr[u].v==3) {//1|
       ans2++;
	   return 1; 
	}
	int r=dfs(tr[u].r);  //如果没走，结果取决于r 
	return r;
}

                  Step4:完整代码

                  #include<iostream>
#include<vector>
#include<stack>
using namespace std;
string s;
const int N=1e6+5;
struct Node{
	int v,l,r;
}tr[N];
int num,ans1,ans2;
stack<char>ops;
stack<int>sta;

vector<char>sf;
void change()// 中缀表达式转后缀表达式 
{
	for(int i=0;i<s.size();i++){
		if(s[i]=='0'||s[i]=='1') sf.push_back(s[i]);   //扫到数字，直接插入sf
		else if(s[i]=='(')  ops.push(s[i]);  //  扫到左边括号，插入运算符栈
		else if(s[i]==')') {
			while(!ops.empty()&&ops.top()!='('){
				sf.push_back(ops.top());// 一直输出到sf。直到遇上( 
				ops.pop();
			}
			ops.pop();  // 输出多余的（ 
		} 
		else if(s[i]=='&'){  //与运算
		     while(!ops.empty()&&ops.top()=='&'){
		     	sf.push_back(ops.top());
		     	ops.pop();
			 }
			 ops.push('&');
	    }
	    else{    //或预算 
	    	while(!ops.empty()&&ops.top()!='('){
		     	sf.push_back(ops.top());
		     	ops.pop();
			 }
			 ops.push('|');
		}
	    
	}
	while (!ops.empty()){
		sf.push_back(ops.top());
		ops.pop();
	}
}
void build()
{
	for(int i=0;i<sf.size();i++){
		if(sf[i]=='1'||sf[i]=='0'){
			tr[++num]={sf[i]-'0',-1,-1};
			sta.push(num);
		}
		else{
			int r=sta.top(); sta.pop();
			int l=sta.top(); sta.pop();
			int v=(sf[i]=='&'?2:3);
			tr[++num]={v,l,r};
			sta.push(num);
		}
	}
}
int dfs(int u)
{
	if(tr[u].v==0||tr[u].v==1) return tr[u].v; //叶子节点 。返回数值 
	int l=dfs(tr[u].l);
	if(l==0&&tr[u].v==2) {//0&
       ans1++;
	   return 0; 
	}
	if(l==1&&tr[u].v==3) {//1|
       ans2++;
	   return 1; 
	}
	int r=dfs(tr[u].r);  //如果没走，结果取决于r 
	return r;
}
int main()
{
	cin>>s;
	change();
	build();
	cout<<dfs(num)<<endl;
	cout<<ans1<<" "<<ans2;
	return 0;
 }
                  • -1
                    @ 2023-3-4 13:40:32

                    思路： (1)将中缀表达式转后缀表达式； (2)转化成表达式树； (3)dfs访问。

                    用vector装后缀表达式，用栈装表达式内的符号（如：'(' '&'等），再用一个字符串（string) 存最初输入的表达式(中缀)。 vector sf; stack ops;

                    ★符号优先级为 () > & > | ；

                    (1) 哪些符号入栈？入栈顺序是？ 1、如果为数字(0或1)，存入sf； 2、如果为 ( ，压入ops； 3、如为 ) ，将ops中与其配对的 ( （也就是最近的'('）之上的运算符全部输出并加到sf，最后删掉配对的 ( （记住右括号不压入栈）；

                    4、如为&(与)，从栈顶弹出所有运算符&加入sf直到碰见 ( 或 | 或栈空； 5、如为 | (或)，从栈顶弹出所有&和|加入sf直到碰见 ( 或 | 或栈空； (接下来重复上面几点直到ops为空）

                    (2) 转化表达式树 建立结构体（node）存放每个节点的值v,及左子树方位l和右子树方位r，再建立栈sta缓存节点位置。 所有非叶节点都为运算符对应的值(我们设&=2，|=3)。

                    (3)dfs

                    1、叶节点返回值(v)； 2、非叶节点通过左子树判断是否为短路(详见题目)，如出现短路，返回左子树值。

                    具体代码： #include<bits/stdc++.h> using namespace std; const int N=1e6+10; vector sf; stack ops; stack sta; struct node{ int v,l,r; }tr[N]; int num,ans1,ans2; string s;

                    void change(){//中缀转后缀 for(int i=0;i<s.size();i++){ if(s[i]'0' || s[i]'1') sf.push_back(s[i]);//插入sf else if(s[i]'('){ ops.push(s[i]);//插入栈 }else if(s[i]')'){ while(!ops.empty() && ops.top()!='('){ sf.push_back(ops.top());//(放入sf尾(?)) 一直输出到sf直到遇到左括号'(' ops.pop(); } ops.pop();//将(也输出掉 }else if(s[i]'&'){//进行与运算 while(!ops.empty() && ops.top()'&'){ sf.push_back(ops.top()); ops.pop(); } ops.push('&');//记得将与压栈 }else{//或运算 while(!ops.empty() && ops.top()!='('){ sf.push_back(ops.top()); ops.pop(); } ops.push('|'); }

                    }

while(!ops.empty()){
	sf.push_back(ops.top());
	ops.pop();
}

                    }

                    void build(){ for(int i=0;i<sf.size();i++){ if(sf[i]'0' || sf[i]'1'){ tr[++num]={sf[i]-'0',-1,-1}; sta.push(num); }else{ int r=sta.top(); sta.pop(); int l=sta.top(); sta.pop(); int v=(sf[i]=='&' ? 2:3); tr[++num]={v,l,r}; sta.push(num); } } }

                    int dfs(int u){ if(tr[u].v0 || tr[u].v1){ return tr[u].v;//叶子节点，返回数值 }

                    int l=dfs(tr[u].l);
if(l==0 && tr[u].v==2){//0&
	ans1++;
	return 0;
}
if(l==1 && tr[u].v==3){//1|
	ans2++;
	return 1;
}

int r=dfs(tr[u].r);//如果没走结果取决于r(后面的数） 
return r;

                    }

                    int main(){ cin>>s; change(); build(); //cout<<1; cout<<dfs(num)<<endl; cout<<ans1<<" "<<ans2<<endl; return 0; }

                    • -1
                      @ 2023-2-23 21:43:14 
                      /*********************************
备注：
*********************************/
#include<map>
#include<list>
#include<stack>
#include<queue>
#include<cmath>
#include<queue>
#include<stack>
#include<deque>
#include<math.h>
#include<cstdio>
#include<string>
#include<vector>
#include<cstring>
#include<fstream>
#include<stdio.h>
#include<sstream>
#include<iomanip>
#include<iostream>
#include<string.h>
#include<algorithm>
#include<bits/stdc++.h>
using namespace std;
#define in int
#define ch char
#define lo long
#define fl float
#define sh short
#define db double
#define ll long long
#define ld long double
#define lli long long int
const int N =1e6+1;
const int INF =0x3f3f3f3f;
char str[N];
int c1[N],c2[N],l1[N],l2[N],cnt1,cnt2;
int dfs(int l,int r)
{
    if(c1[r]>=l)
	{
        int ans=dfs(l,c1[r]-1);
        if (ans==1)
		{
            ++cnt1;
            return 1;
        }
        return (ans|dfs(c1[r]+1,r));
    }
    if(c2[r]>=l)
	{
        int ans=dfs(l,c2[r]-1);
        if (ans==0)
		{
            ++cnt2;
            return 0;
        }
        return (ans&dfs(c2[r]+1,r));
    }
    if (str[l]=='('&&str[r]==')')
	{
        return dfs(l+1,r-1);
    }
    return str[l]-'0';
}
int main(int argc, const char * argv[])
{
    scanf("%s",str + 1);
    int len=strlen(str+1);
    int x=0; 
    for(int i=1;i<=len;i++)
	{
        if(str[i]=='(')
		{
            x++;
        }
		else if(str[i]==')')
		{
            --x;
        }
		else if(str[i]=='|')
		{
            l1[x]=i;
        }else if(str[i]=='&')
		{
            l2[x]=i;
        }
        c1[i]=l1[x];
        c2[i]=l2[x];
    }
    int ans=dfs(1,len);
    cout<<ans<<endl<<cnt2<<" "<<cnt1;
    return 0;
}
                      • 1

                      「CSP-J 2022」逻辑表达式（expr）

                      信息

                      ID
                      2918
                      时间
                      1000ms
                      内存
                      256MiB
                      难度
                      8
                      标签
                      递交数
                      156
                      已通过
                      48
                      上传者
                      1. 关于
                      2. 联系我们
                      3. 隐私
                      4. 服务条款
                      5. 版权申诉
                      6. Language
                      7. 兼容模式
                      8. 主题
                      3. Worker 0, 164ms
                      4. Powered by Hydro v4.19.1 Community