此题重点在二分图的建图。

考虑放置木板的决策，由于可以重复覆盖，所以对于两个可以选择的区间 a,b**，若 b** 被 a** 覆盖，那么选择 a** 一定优于选择 b**。

解释如图：泥地为黄色，草地为绿色

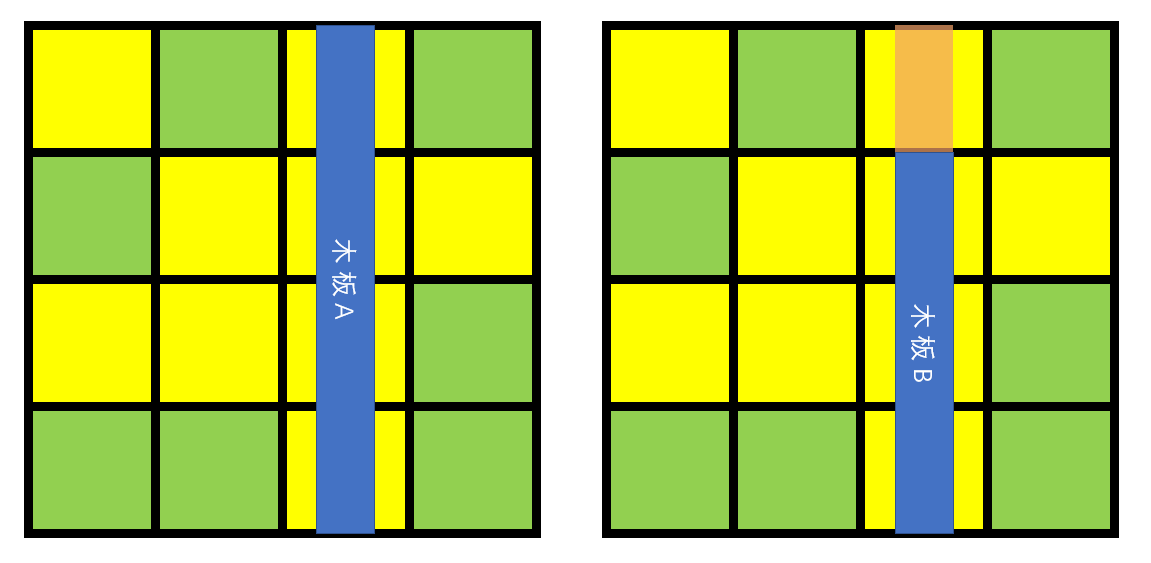
显然，木板 A 一定比木板 B 更优，因为橙色部分可以重复覆盖。

由此易得所有的木板两头都是没有泥地的：若有，则增长此木板一定比原方案更优。

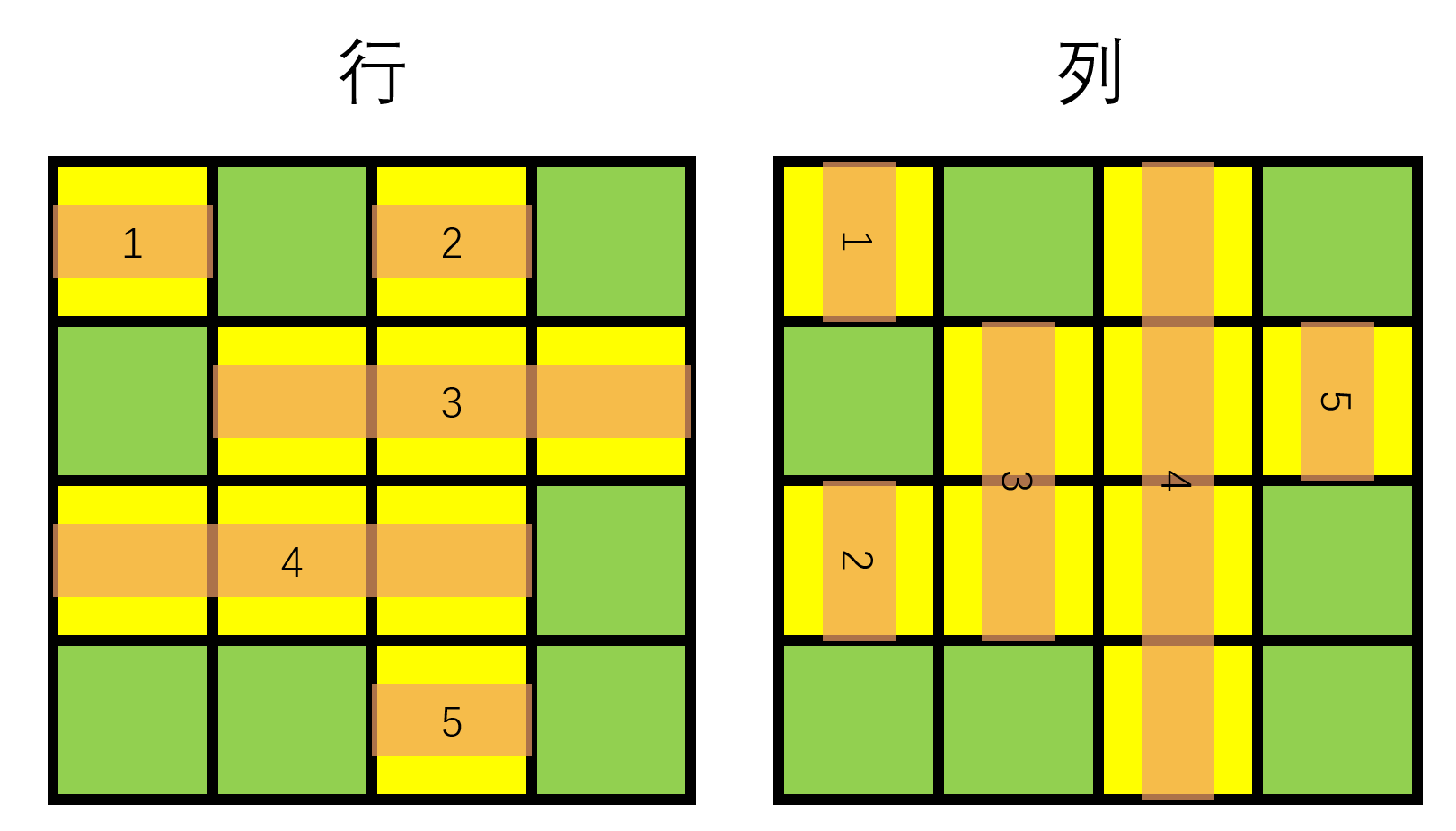
得到这个结论，我们可以先预处理出所有可能放置木板的位置，也就是在每行每列连续的泥地的位置。如图所示：所有木板可能放置的位置是下图的十个。

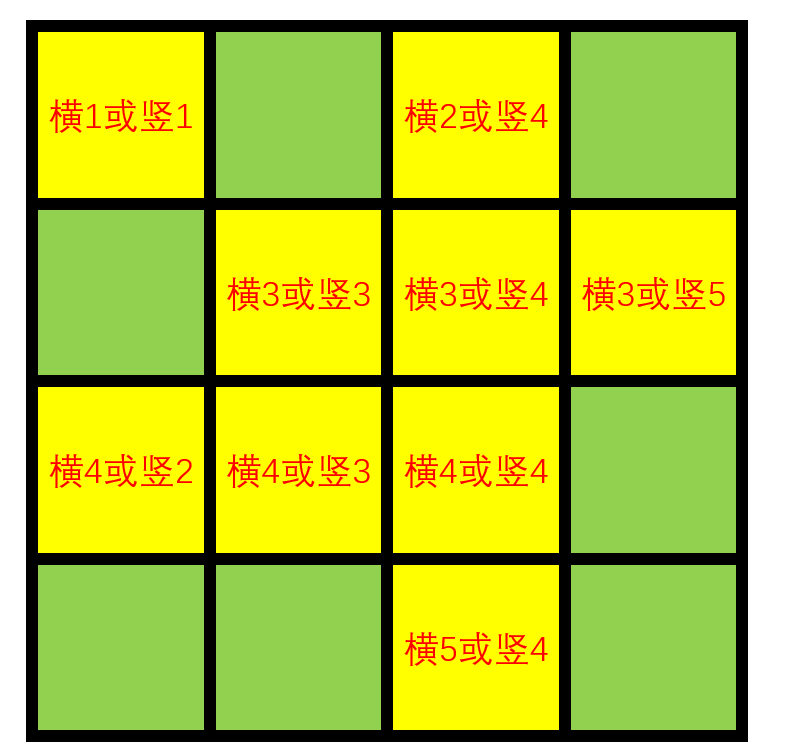
对于每一个点，要么被横着覆盖，要么被竖着覆盖。举例来讲，(3,3)** 在行上会被横木板 3覆盖，在列上会被竖木板 4 覆盖。而我们要让所有的点都被覆盖，也就是需要满足下图所示的所有条件：

我们需要选出最少的木板满足这样的若干个约束条件。我们把每一个泥地看成一条边，左端点为其对应的横木板，右端点为其对应的竖木板。 显然这是一个二分图，左边全部为横木板，右边全部为竖木板。

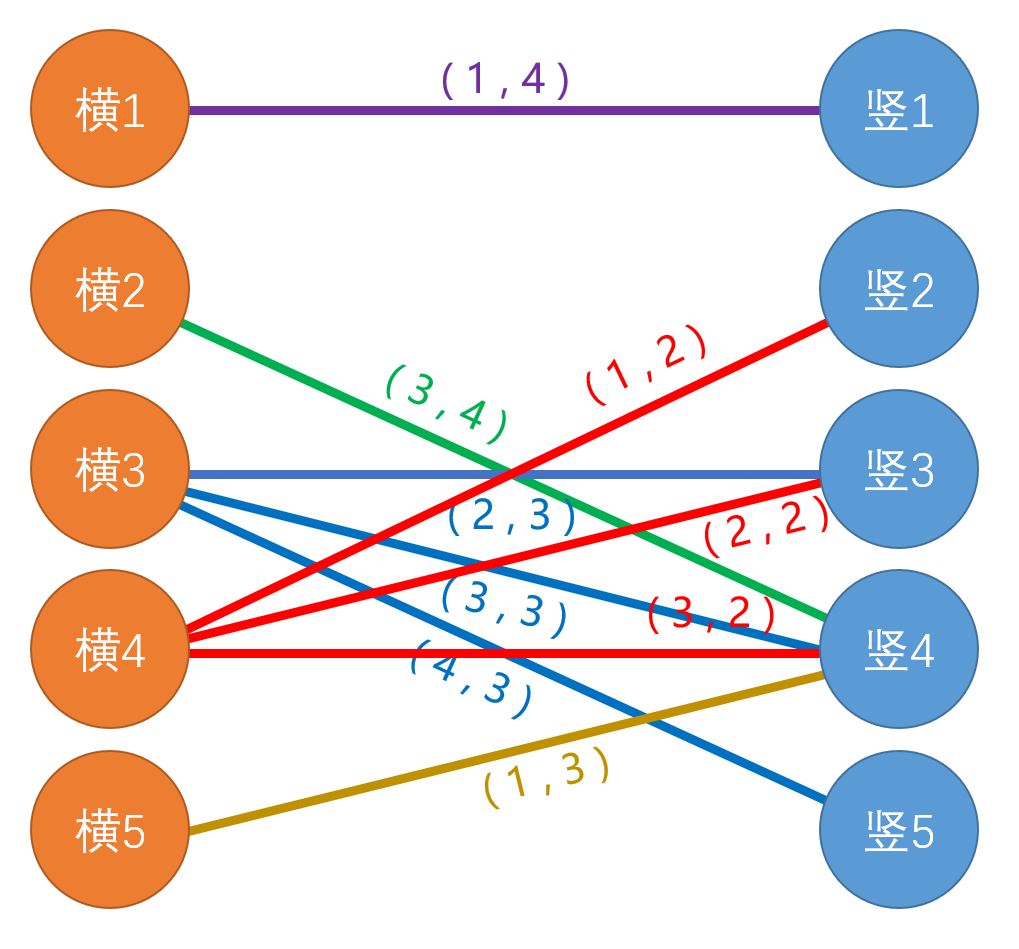
考虑我们 放置一个木板 ，相当于满足所有包含它的约束条件， 也就是将其所连的边进行染色 。 而对于每一个泥地（也就是边）， 如果它被染色，就证明这个格子的约束条件已被满足 。

所以这个问题转化为：一次操作可以选择一个点，将所连的边染色，目的是让所有边被染色。

即为二分图最小点覆盖。

而最小点覆盖等于最大匹配，故建图跑匈牙利即可。

代码：

#include<bits/stdc++.h>
using namespace std;
int n,m;
int cnt1,cnt2;
bool a[1002][1002];
int match[1002];
int ans;
bool visit[1002];
bool dfs(int x){
	for(int i=1;i<=cnt2;i++){
		if(a[x][i]&&!visit[i]){
			visit[i]=1;
			if(!match[i]||dfs(match[i])){
				match[i]=x;
				return 1;
			}
		}
	}
	return 0;
}
char ch[1002][1002];
int h[1002][1002];
int c[1002][1002];
int main(){
	cin>>n>>m;
	for(int i=1;i<=n;i++){//统计横向木板 
		cin>>ch[i]+1;
		for(int j=1;j<=m;j++){
			if(ch[i][j]=='*'){
				if(j==1||ch[i][j-1]!='*'){
					h[i][j]=++cnt1;
				}
				else h[i][j]=cnt1;
			}
		}
	}
	for(int i=1;i<=m;i++){//统计竖向木板 
		for(int j=1;j<=n;j++){
			if(ch[j][i]=='*'){
				if(j==1||ch[j-1][i]!='*'){
					c[j][i]=++cnt2;
				}
				else c[j][i]=cnt2;
				a[h[j][i]][c[j][i]]=1;
			}
		}
	}
	for(int i=1;i<=cnt1;i++){//跑匈牙利 
		memset(visit,0,sizeof visit);
		ans+=dfs(i);
	}
	cout<<ans;
	return 0;
}

本文章选自洛谷tj