#3173. 日记和二叉搜索树
日记和二叉搜索树
题目限制
2000 ms 1024 M
题目描述
题目背景
日记今天学习了二叉搜索树。二叉搜索树上,对于一个节点,它的左子树上每个点的点权都小于它的点权,它的右子树上每个点的点权都大于它的点权。
题目描述
日记很喜欢二叉搜索树,所以她想把这种性质扩展到一般的树上。
现有一棵以节点 为根的树,她给树上每一个节点钦定了一个不同的点权 。
她认为一对节点 是好的,当且仅当 ,其中 为 的最近公共祖先。
现在,她想让这棵树尽可能的好,也就是让好的节点对数最多。
额外地,她认为排列是美观的,因此她要求点权 构成一个 的排列。
请输出好的节点对数的最大值。
输入格式
第 行, 个正整数 ,代表树有 个节点。
接下来 行,每行 个正整数 ,代表树上有一条连接 的边。
保证输入构成一棵树。
输出格式
输出 行 个非负整数,为好的节点对数的最大值。
数据范围
本题设置 50 个测试点,每个测试点 2 分。我们称一个测试点的 为其编号 。同时,每个测试点满足一些限制,见下:
| 特殊性质 | ||
|---|---|---|
特别地,特殊性质 s(x) 代表:对每个节点,其儿子节点个数不超过 ;h(x) 代表:若钦定根节点深度为 ,每个节点的深度为其父节点深度 ,则节点的深度最大值不超过 ;r 代表:数据随机生成,即 的父亲在 中等概率随机选取。
对全部数据,有 。
输入样例 1
5
1 2
2 3
1 4
4 5
输出样例 1
4
输入样例 2
6
1 2
2 3
2 4
1 5
5 6
输出样例 2
7
样例解释
对于样例 ,此处给出一种存在 对好的节点的构造,其中括号前的数为节点编号,括号内的数为权值 :
.png)
可以证明,不存在一种构造使得好的节点的对数 。
样例 的一种构造:
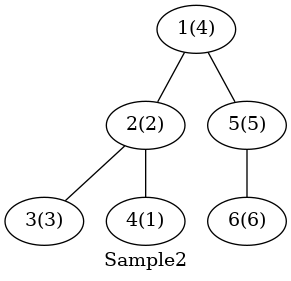
相关
在下列比赛中:
