#2986. 宿舍楼
宿舍楼
题目描述
某 中学的宿舍楼有 层(由 到 表示),每层楼可以均分为 个宿舍(由 到 表示)。
同时,除顶楼外,每层楼都有恰好 个楼梯通向上一层。如果一个楼梯下端在 层 号宿舍门前,它的上端就在 层的 宿舍门前。
一个人在宿舍里行走,有如下几种可能:
- 左右行走,从第 层 号宿舍门前走到 层 号或 号宿舍门前,花费 秒;
- 上下行走,如果有连接第 层 号和第 层 号的楼梯,他就可以从第 层 号上到 层(或正好相反),需要花费 秒。
C 教练有 名学生,第 名学生住在第 层 号宿舍。有一天,C 教练来到第 层 号宿舍门前,要求所有学生来此集中。听到广播后,所有学生同时走出宿舍门,并按照耗时最少的路线行进。学生走出宿舍门的时间不计。
请问,每个学生走到 C 教练所在地分别需要多少秒?
输入格式
第 行有 个正整数 ,表示宿舍楼有 层 号,C 教练有 个学生。
接下来有 行,第 行有 个正整数 ,表示连接第 层与第 层的楼梯的位置。
接下来有 行,第 行有 个正整数 表示 C 教练的第 个学生住在第 层 号宿舍。
输出格式
输出 行,每行 个非负整数。第 行的表示第 个学生从宿舍走到 C 教练所在地需要花费多少秒的时间。
4 11 5
3 6 10
1 5 8
2 3 4
1 1
2 3
3 4
4 3
4 11
0
4
9
12
18
样例解释
宿舍结构如下图所示,从下往上为 到 层,从左往右为 到 号。
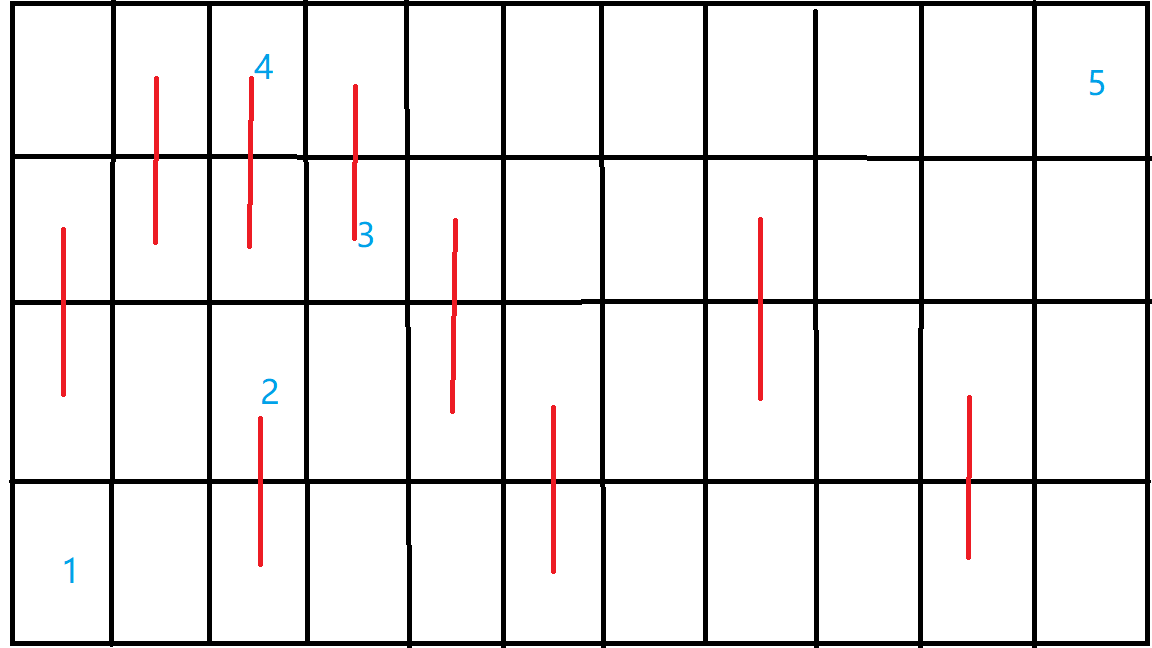
其中,红线表示两地间有楼梯连接,蓝色数字表示第 个学生住在这里。
下文“从第 层 号下楼”表示从第 层 号走到第 层 号,当然,要花费 秒。
可以发现,第 个学生只需走出宿舍即可到达 C 教练所在地,花费 秒;
第 个学生可以从第 层 号下楼,花费 秒,然后往左走,花费 秒,总共花费 秒。
第 个学生可以往右走到第 层 号下楼,然后往左走到第 层 号下楼,然后往左走,总共花费 秒。
第 个学生从第 层 号下楼,然后既可以从第 层 号下楼,也可以从第 层 号下楼,总共花费 秒。
第 个学生从第 层 号下楼,然后路径同第 号学生一致,总共花费 秒。
数据范围
对于前 数据,;
对于所有的数据,,,,,,。
